Cho mạch điện xoay chiều RLC mắc nối tiếp
Câu hỏi :
Cho mạch điện xoay chiều RLC mắc nối tiếp. Đặt vào hai đầu đoạn mạch một điện áp xoay chiều u = U0cosωt (u đo bằng V; ω có thể thay đổi). Đồ thị sự phụ thuộc của cường độ dòng điện hiệu dụng vào ω như hình vẽ. Biết ω2 – ω1 = 400/π rad/s, L = 3π/4(H). Giá trị điện trở thuần R của mạch bằng: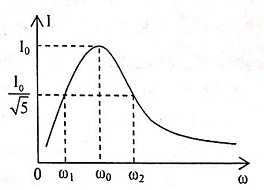
A. 200 W
B. 160 W
C. 150 W
D. 100 W
* Đáp án
C
* Hướng dẫn giải
+ Từ đồ thị nhận thấy có hai giá trị ω1 và ω2 cho cùng
\(\begin{array}{l}
{I_1} = {I_2} = \frac{{{I_{\max }}}}{{\sqrt 5 }} = \frac{U}{{\sqrt 5 R}}\\
\Rightarrow \frac{U}{{\sqrt {{R^2} + {{\left( {{\omega _1}L - \frac{1}{{{\omega _1}C}}} \right)}^2}} }} = \frac{U}{{\sqrt 5 R}}\\
\Rightarrow 5{R^2} = {R^2} + {\left( {{\omega _1}L - \frac{1}{{{\omega _1}C}}} \right)^2}\\
\Rightarrow \left| {{\omega _1}L - \frac{1}{{{\omega _1}C}}} \right| = 2R
\end{array}\) (1)
+ Mặt khác: \({I_1} = {I_2} \Rightarrow {\omega _1}{\omega _2} = \frac{1}{{LC}} \Rightarrow {\omega _2}L = \frac{1}{{{\omega _1}C}}\) (2)
+ Thay (2) vào (1), ta có:
\(R = \frac{{L\left| {{\omega _1} - {\omega _2}} \right|}}{2} = \frac{{\frac{{3\pi }}{4}.\frac{{400}}{\pi }}}{2} = 150\Omega \)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Trần Xuân Soạn
Copyright © 2021 HOCTAP247
