Một con lắc đơn gồm m treo vào dây l tại nơi có gia tốc trọng trường g
Câu hỏi :
Một con lắc đơn gồm vật khối lượng m treo vào dây có chiều dài l tại nơi có gia tốc trọng trường g. Đầu kia của dây được gắn với bộ cảm biến để có thể đo lực căng của dây theo phương thẳng đứng. Kéo con lắc lệch khỏi vị trí cân bằng góc α0 rồi thả nhẹ. Đồ thị biểu diễn sự biến thiên độ lớn lực căng dây theo phương thẳng đứng theo thời gian như hình vẽ. Khối lượng của vật treo gần giá trị nào nhất sau đây?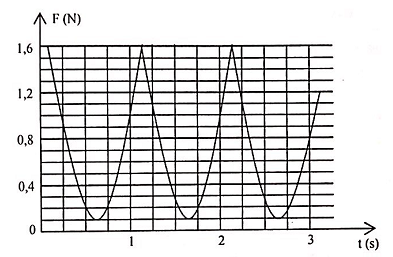
A. 105 g
B. 73 g
C. 96 g
D. 87 g
* Đáp án
B
* Hướng dẫn giải
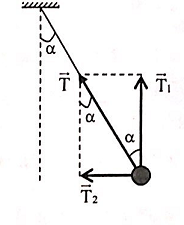
+ Lực căng dây: T = mg(3cosα - 2cosα0)
+ Lực căng dây theo phương thẳng đứng:
\({T_1} = T\cos \alpha = mg\left( {3\cos \alpha - 2\cos {\alpha _0}} \right)\cos \alpha \Rightarrow \left\{ \begin{array}{l}
{T_{l\max }} = mg\left( {3 - 2\cos {\alpha _0}} \right)\\
{T_{l\min }} = mg{\cos ^2}{\alpha _0}
\end{array} \right.\)
+ Theo đồ thị:
\(\begin{array}{l}
\left\{ \begin{array}{l}
{T_{l\max }} = 1,6 = mg\left( {3 - 2\cos {\alpha _0}} \right)\\
{T_{l\min }} = 0,1 = mg{\cos ^2}{\alpha _0}
\end{array} \right.\\
\Rightarrow \left\{ \begin{array}{l}
{T_{l\max }} = 1,6 = mg\left( {3 - 2\cos {\alpha _0}} \right)\\
{T_{l\min }} = 0,1 = mg{\cos ^2}{\alpha _0}
\end{array} \right. \Rightarrow 16 = \frac{{3 - 2\cos {\alpha _0}}}{{{{\cos }^2}{\alpha _0}}}\\
\Rightarrow 16{\cos ^2}{\alpha _0} + 2\cos {\alpha _0} - 3 = 0 \Rightarrow \cos {\alpha _0} = \frac{3}{8}
\end{array}\)
+ Ta có:
\(m = \frac{{{T_{l - \max }}}}{{g\left( {3 - 2\cos {\alpha _0}} \right)}} = \frac{{1,6}}{{9,8\left( {3 - 2.\frac{3}{8}} \right)}} = 0,073kg = 73g\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Trần Xuân Soạn
Copyright © 2021 HOCTAP247
