Đặt điện áp xoay chiều u=U√2cos(ωt + φ) (V) (với U và ω không đổi)
Câu hỏi :
Đặt điện áp xoay chiều u=U√2cos(ωt + φ) (V) (với U và ω không đổi) vào hai đầu đoạn mạch AB nối tiếp gồm điện trở thuần R, cuộn dây không thuần cảm (có điện trở r), tụ điện, theo thứ tự đó. Biết R = r. Gọi M là điểm nối giữa R và cuộn dây, N là điểm nối giữa cuộn dây và tụ điện. Đồ thị biểu diễn điện áp uAN và uMB như hình vẽ bên. Giá trị của U gần nhất với giá trị nào sau đây: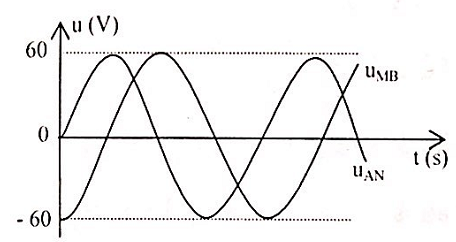
A. 76 V
B. 42 V
C. 85 V
D. 54 V
* Đáp án
D
* Hướng dẫn giải
Ta có:
\(\begin{array}{l}
\left\{ \begin{array}{l}
{u_{AN}} = 60\cos \left( {\omega t - \frac{\pi }{2}} \right)\left( V \right)\\
{u_{MB}} = 60\cos \left( {\omega t + \pi } \right)\left( V \right)
\end{array} \right. \Rightarrow {u_{AN}} \bot {u_{MB}}\\
\Rightarrow \tan {\varphi _{AN}}.\tan {\varphi _{MB}} = - 1\\
\Leftrightarrow \frac{{{Z_L}}}{{2R}}.\frac{{{Z_L} - {Z_C}}}{R} = - 1\\
\Leftrightarrow {Z_L}\left( {{Z_C} - {Z_L}} \right) = 2{R^2}
\end{array}\) (1)
+ Lại có:
\({U_{AN}} = {U_{MB}} \Leftrightarrow 4{R^2} + Z_L^2 = {R^2} + {\left( {{Z_L} - {Z_C}} \right)^2} \Rightarrow 3{R^2} = Z_C^2 - 2{Z_L}{Z_C}\) (2)
+ Từ (1) và (2), ta có:
\( \Rightarrow \left\{ \begin{array}{l}
{Z_C} = 3{Z_L}\\
{Z_C} = 0,5{Z_L}
\end{array} \right.{Z_C} = 3{Z_L}R = {Z_L} \Rightarrow {Z_C} = 3R\)
+ Mặt khác, ta có:
\(\begin{array}{l}
{U_{AN}} = 60 = \frac{{U\sqrt {4{R^2} + Z_L^2} }}{{\sqrt {4{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} }}\\
60 = \frac{{{U_0}\sqrt {4{R^2} + {R^2}} }}{{\sqrt {4{R^2} + 4{R^2}} }}\\
\Rightarrow {U_0} = 24\sqrt {10} \Rightarrow U \approx 54\left( V \right)
\end{array}\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Lương Hữu Phước
Copyright © 2021 HOCTAP247
