Đồ thị dòng điện trong mạch dao động điện từ LC lý tưởng như hình vẽ bên
Câu hỏi :
Đồ thị dòng điện trong mạch dao động điện từ LC lý tưởng như hình vẽ bên. Biểu thức điện tích trên tụ điện là: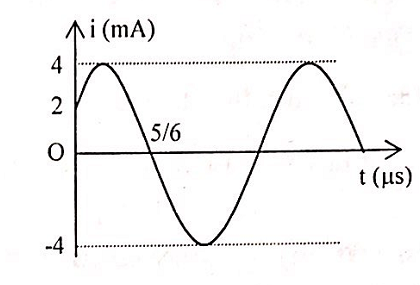
A. \(4\pi \cos \left( {\pi {{.10}^6}t + \frac{\pi }{6}} \right)\) (nC).
B. \(4\pi \cos \left( {\pi {{.10}^7}t - \frac{{5\pi }}{6}} \right)\) (µC).
C. \(40\pi \cos \left( {\pi {{.10}^6}t + \frac{\pi }{6}} \right)\) (µC).
D. \(0,4\cos \left( {\pi {{.10}^6}t - \frac{{5\pi }}{6}} \right)\) (nC).
* Đáp án
D
* Hướng dẫn giải
+ Tại t = 0 => i = 2 mA và đang tăng => \({\varphi _i} = - \frac{\pi }{3}\)rad
+ Thời gian từ khi i=2 và đang tăng đến khi i = 0 là:
\(\begin{array}{l}
\Delta t = \frac{T}{6} + \frac{T}{4} = \frac{5}{6}{.10^6}\\
\Rightarrow T = {2.10^{ - 6}}\left( s \right) \Rightarrow \omega = {10^6}\pi \left( {rad/s} \right)
\end{array}\)
+ Biểu thức dòng điện:
\(\begin{array}{l}
i = {4.10^{ - 3}}\cos \left( {\pi {{.10}^6} - \frac{\pi }{3}} \right)A\\
\Rightarrow {Q_0} = \frac{{{I_0}}}{\omega } = \frac{{{{4.10}^{ - 3}}}}{{\pi {{10}^6}}} = \frac{4}{\pi }{.10^{ - 9}}\left( C \right) = \frac{4}{\pi }\left( {nC} \right) = 0,4\pi \left( {nC} \right)
\end{array}\)
+ Vì điện tích q trễ pha với i nên biểu thức điện tích trên tụ là:
\(q = 0,4\pi \cos \left( {\pi {{.10}^6}t - \frac{\pi }{3} - \frac{\pi }{2}} \right) = 0,4\pi \cos \left( {\pi {{.10}^6}t - \frac{{5\pi }}{6}} \right)\) (nC)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Đặng Trần Côn
Copyright © 2021 HOCTAP247
