Một đu quay có bán kính R=2√3m, lồng bằng kính trong suốt quay đều

* Hướng dẫn giải

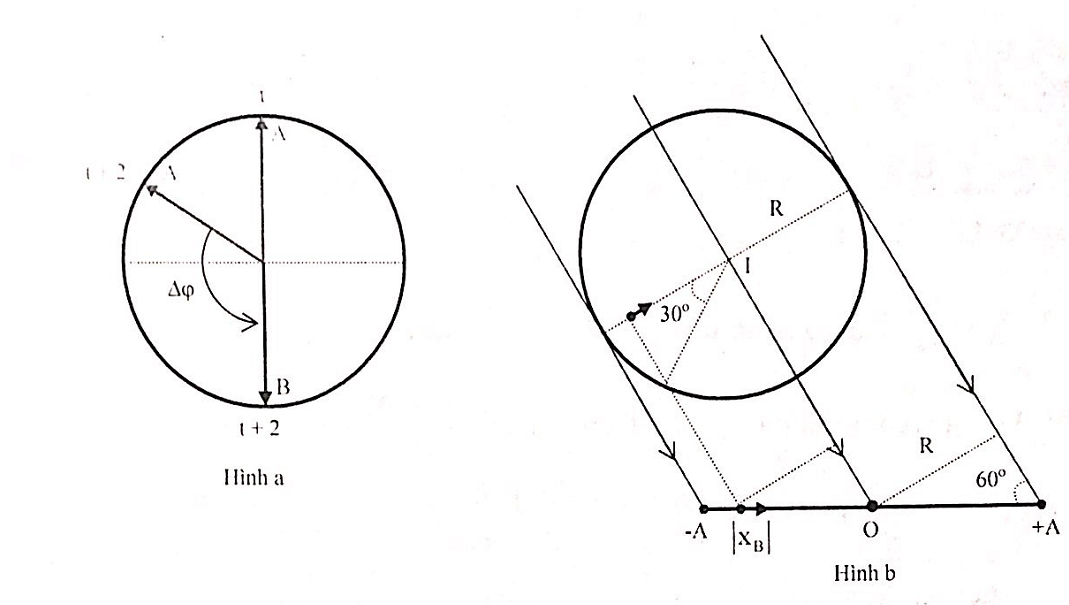
Ở thời điểm t (s) người A thấy mình ở vị trí cao nhất, đến thời điểm t + 6(s) lại thấy mình ở vị trí thấp nhất nên ta có:

\(\frac{T}{2} = 6 \Rightarrow T = 12\left( s \right) \Rightarrow \omega  = \frac{{2\pi }}{T} = \frac{\pi }{6}\) (rad/s)

+ Tại thời điểm t người A ở cao nhất, sau Δt = 2(s) người A quay thêm góc

\(\alpha  = \omega \Delta t = \frac{\pi }{6}.2 = \frac{\pi }{3}\) 

+ Lúc này người B đang ở vị trí thấp nhất. Từ hình vẽ a suy ra người B nhanh pha hơn người A góc 2π/3 (rad)

+ Từ hình vẽ b, bóng người trên mặt đất dao động với biên độ là:

\(A = \frac{R}{{\sin 60^\circ }} = \frac{{2\sqrt 3 }}{{\sin 60^\circ }} = 4\) (cm)

+ Khi bóng của A đi qua O thì bóng của B có li độ |xB|.

+ Theo hình vẽ, ta có:  

\(\begin{array}{l}
\sin 60^\circ  = \frac{{R\cos 30^\circ }}{{\left| {{x_B}} \right|}}\\
 \Rightarrow \left| {{x_B}} \right| = \frac{{R\cos 30^\circ }}{{\sin 60^\circ }} = \frac{{2\sqrt 3 \cos 30^\circ }}{{\sin 60^\circ }} = 2\sqrt 3 
\end{array}\) 

+ Theo công thức độc lập ta có:

\(v_B^/ = \omega \sqrt {{A^2} - {{\left( {x_B^/} \right)}^2}}  = \frac{\pi }{6}\sqrt {{4^2} - {{\left( {2\sqrt 3 } \right)}^2}}  = \frac{\pi }{3}\) (m/s)

+ Vì đang lại gần O nên suy ra tốc độ đang tăng