Một chất điểm DĐĐH. Đồ thị biểu diễn li độ phụ thuộc vào t như hình vẽ.
Câu hỏi :
Một chất điểm DĐĐH. Đồ thị biểu diễn li độ phụ thuộc vào thời gian như hình vẽ. Biết t3 + 2t1 – 3t2 = 0 và tốc độ trung bình của chất điểm từ thời điểm ban đầu đến thời điểm t1 là 6 cm/s. Viết phương trình dao động của chất điểm.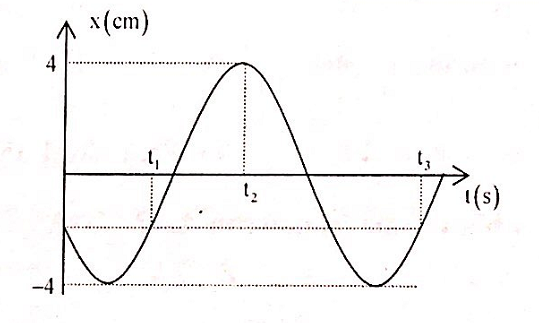
A. \(x = 4\cos \left( {\pi t + \frac{{5\pi }}{6}} \right)\) (cm)
B. \(x = 4\cos \left( {\pi t + \frac{{3\pi }}{4}} \right)\) (cm)
C. \(x = 4\cos \left( {\pi t - \frac{{2\pi }}{3}} \right)\) (cm)
D. \(x = 4\cos \left( {\pi t + \frac{{2\pi }}{3}} \right)\) (cm)
* Đáp án
D
* Hướng dẫn giải
+ Gọi Δt là thời gian ngắn nhất chất điểm đi từ vị trí ban đầu x0 đến biên âm.
+ Từ đồ thị, ta có:
\(\left\{ \begin{array}{l}
{t_1} = 2\Delta t\\
{t_2} = \frac{T}{2} + \Delta t\\
{t_3} = T + 2\Delta t
\end{array} \right.\)
+ Mặt khác:
\(\begin{array}{l}
{t_3} + 2{t_1} - 3{t_2} = 0\\
\Leftrightarrow T = 2\Delta t + 4\Delta t - \frac{{3T}}{2} - 3\Delta t = 0 \Rightarrow \Delta t = \frac{T}{6}\\
\Rightarrow {x_0} = - \frac{A}{2} = - 2\left( {{\rm{cm}}} \right) - 2 = 4\cos \varphi \\
\Rightarrow \varphi = \pm \frac{{2\pi }}{3}\varphi = \frac{{2\pi }}{3}
\end{array}\)
+ Phương trình:
\(\begin{array}{l}
\overline v = \frac{{{s_1}}}{{{t_1}}} = \frac{{2 + 2}}{{2.\frac{T}{6}}} \Leftrightarrow 6 = \frac{{12}}{T}\\
\Rightarrow T = 2\left( s \right) \Rightarrow \omega = \pi (rad/s)\\
x = 4\cos \left( {\pi t + \frac{{2\pi }}{3}} \right)cm
\end{array}\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Nguyễn Thị Minh Khai
Copyright © 2021 HOCTAP247
