Trang chủ
Đề thi & kiểm tra
Lớp 12
Vật lý
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Lục Nam
Một con lắc đơn dao động theo pt \(s=4\cos \left(...
Một con lắc đơn dao động theo pt \(s=4\cos \left( 2\pi t \right)\,\)cm
Câu hỏi :
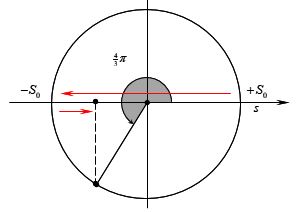
Một con lắc đơn dao động theo phương trình \(s=4\cos \left( 2\pi t \right)\,\)cm (t tính bằng giây). Quãng đường mà con lắc này đi được trong khoản thời gian \(\Delta t=\frac{2}{3}\)s là
A. 10 cm.
B. 8 cm.
C. 20 cm.
D. 14 cm.
* Đáp án
A
* Hướng dẫn giải
Ta có:
\(t=0\) thì vật đang ở vị trí biên dương.
\(\Delta t=\frac{2}{3}\)s → \(\Delta \varphi =\omega \Delta t=\left( 2\pi \right)\left( \frac{2}{3} \right)=\pi +\frac{\pi }{3}\).
\(S=2,5{{S}_{0}}=2,5.\left( 4 \right)=10\)cm.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Lục Nam
Số câu hỏi: 39
Copyright © 2021 HOCTAP247