Trang chủ
Đề thi & kiểm tra
Lớp 12
Vật lý
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Thái Thuận
Đặt điện áp \(u=50\cos (\omega t+\varphi )\) ω do không...
Đặt điện áp \(u=50\cos (\omega t+\varphi )\) ω do không đổi
Câu hỏi :
Đặt điện áp \(u=50\cos (\omega t+\varphi )\) (ω do không đổi \(\frac{\pi }{4}<\varphi <\frac{\pi }{2})\) vào hai đầu đoạn mạch mắc nối tiếp theo thứ tự: điện trở R, cuộn cảm thuần L với \({{Z}_{L}}=\sqrt{3}R\)và tụ điện có điện dung C thay đổi được. Khi \(C={{C}_{1}}\) thì điện áp hiệu dụng giữa hai đầu tụ điện là cực đại và \({{u}_{C1}}=100\cos (\omega t)V.\) Khi \(C={{C}_{2}}\)thì điện áp giữa hai đầu đoạn mạch chữa R và L là \({{u}_{2}}={{U}_{0}}\cos \left( \omega t+\frac{\pi }{2} \right)V.\) Giá trị của U0 gần nhất giá trị nào sau đây
A. 60V
B. 26V
C. 87V
D. 78V
* Đáp án
C
* Hướng dẫn giải
Ta có giản đồ vecto:
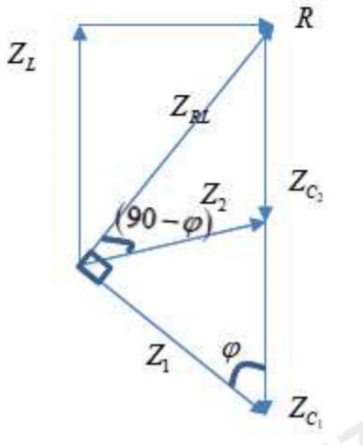
Ta có \(\frac{{{U}_{0{{C}_{1}}}}}{{{U}_{0AB}}}=\frac{100}{50}=\frac{{{Z}_{{{C}_{1}}}}}{{{Z}_{1}}}=\frac{1}{\cos \varphi }\)
\(\Rightarrow \cos \varphi =\frac{1}{2}\Rightarrow \varphi ={{60}^{0}}\)
Lại có: \(\frac{{{U}_{0}}}{{{U}_{0AB}}}=\frac{{{U}_{0}}}{50}=\frac{{{Z}_{RL}}}{{{Z}_{2}}}=\sqrt{3}\Rightarrow {{U}_{0}}=50\sqrt{3}V\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Thái Thuận
Số câu hỏi: 40
Copyright © 2021 HOCTAP247
