Trang chủ
Đề thi & kiểm tra
Lớp 12
Vật lý
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Thái Thuận
Hai con lắc lò xo có \({{k}_{1}}={{k}_{2}}=k;\)
Hai con lắc lò xo có \({{k}_{1}}={{k}_{2}}=k;\)
Câu hỏi :
Hai con lắc lò xo có \({{k}_{1}}={{k}_{2}}=k;\) vật nặng cùng khối lượng \({{m}_{1}}={{m}_{2}}=m\)(như hình vẽ). Hai vật đặt sát nhau, khi hệ nằm cân bằng các lò xo không biến dạng, chọn trục tọa độ từ M đến N, gốc là vị trí cân bằng. Ban đầu hệ dao động điều hòa không ma sát trên mặt phẳng nằm ngang với biên độ 8cm. Khi hai vật ở vị trí biên âm thì người ta nhẹ nhàng tháo lò xo kra khỏi hệ, sau khi về vị trí cân bằng thì \({{m}_{2}}\) tách rời khỏi \({{m}_{1}}\)cho rằng khoảng MN đủ dài để mg chưa chạm tường. Khi vật \({{m}_{1}}\)dừng lại lần đầu tiên thì khoảng cách từ \({{m}_{1}}\) đến \({{m}_{2}}\)bằng 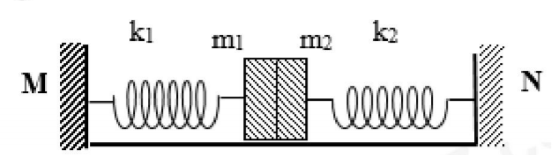
A. 1,78cm
B. 3,2cm
C. 0,45cm
D. 0,89cm
* Đáp án
B
* Hướng dẫn giải
+ Biên độ dao động: A= 8cm
+ Ban đầu: \({{v}_{1}}={{v}_{2}}=\omega A=\sqrt{\frac{k}{{{m}_{1}}+{{m}_{2}}}}\cdot A=\sqrt{\frac{k}{2m}}A\)
Thời gian vật đi từ VTCB đến biên lần đầu: \(\Delta t=\frac{{{T}'}}{4}=\frac{2\pi \sqrt{\frac{m}{k}}}{4}\)
Vật (2) khi đó chuyển động thẳng đều trong khoảng thời gian \(\Delta t\)
Ta có, quãng đường vật (2) đi được:
\(S={{v}_{2}}\Delta t=\sqrt{\frac{k}{2m}}.A.\frac{{{T}'}}{4}=\sqrt{\frac{k}{2m}}.8.\frac{2\pi }{4}\sqrt{\frac{m}{k}}=2\sqrt{2}\pi (m)\)
Khoảng cách cần tìm: \(S-{A}'=2\sqrt{2}\pi -4\sqrt{2}=3,23cm\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Thái Thuận
Số câu hỏi: 40
Copyright © 2021 HOCTAP247
