Hai chất điểm M và N dao động điều hòa dọc theo hai đường thẳng song song

* Hướng dẫn giải

Từ \(\frac{x_{1}^{2}}{36}+\frac{x_{2}^{2}}{64}=1\) ta suy ra được

\(\left\{ \begin{align} & \frac{x_{1}^{2}}{36}\le 1 \\ & \frac{x_{2}^{2}}{64}\le 1 \\ \end{align} \right.\)

\(\Rightarrow \left\{ \begin{align} & -6\le {{x}_{1}}\le 6 \\ & -8\le {{x}_{2}}\le 8 \\ \end{align} \right.\)

\(\Rightarrow \left\{ \begin{align} & {{A}_{1}}=6\left( cm \right) \\ & {{A}_{2}}=8\left( cm \right) \\ \end{align} \right.\)

Ta có:

\(A_{1}^{2}=x_{1}^{2}+\frac{v_{1}^{2}}{{{\omega }^{2}}}\Leftrightarrow {{6}^{2}}={{\left( -3\sqrt{2} \right)}^{2}}+\frac{{{\left( 60\sqrt{2} \right)}^{2}}}{{{\omega }^{2}}}\Rightarrow \omega =20\left( rad/s \right)\)

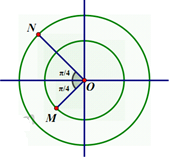
Sử dụng vòng tròn đơn vị: tại thời điểm t, li độ \({{x}_{1}}=\frac{-{{A}_{1}}\sqrt{2}}{2}\)

\({{v}_{1}}>0\)nên ta có điểm M trên hình vẽ. Theo đề bài, N dao động chậm pha hơn M là π/2 nên ta có N như trên hình.

Từ hình vẽ ta suy ra :

\({{x}_{2}}=\frac{-{{A}_{2}}\sqrt{2}}{2}=-4\sqrt{2}\,\left( cm \right)\) và \({{v}_{2}}=\frac{-{{A}_{2}}\omega \sqrt{2}}{2}=-80\sqrt{2}\left( cm/s \right)\)

Vận tốc tương đối: 

\(\left| {{v}_{td}} \right|=\left| {{v}_{1}}-{{v}_{2}} \right|=140\sqrt{2}\,\left( cm/s \right)\)