Đặt điện áp \(u=220\sqrt{2}\cos \left( 100\pi t+\varphi \right)\)(V)
Câu hỏi :
Đặt điện áp \(u=220\sqrt{2}\cos \left( 100\pi t+\varphi \right)\)(V) vào hai đầu đoạn mạch AB chứa RLC nối tiếp theo đúng thứ tự đó, điện dung C thay đổi sao cho dòng điện qua mạch có biểu thức \(i={{I}_{0}}\cos 100\pi t\left( A \right)\). Gọi M là điểm nối giữa cuộn cảm L và tụ điện C. Biết biểu thức điện áp giữa hai đầu đoạn mạch AM, MB lần lượt là \({{u}_{1}}={{U}_{01}}\cos \left( 100\pi t+\frac{\pi }{3} \right)V\), \({{u}_{2}}={{U}_{02}}\cos \left( 100\pi t-\frac{\pi }{2} \right)V\). Tổng \(\left( {{U}_{01}}+{{U}_{02}} \right)\) có giá trị lớn nhất là
A. 750 V
B. 1202 V
C. 1247 V
D. 1242 V
* Đáp án
B
* Hướng dẫn giải
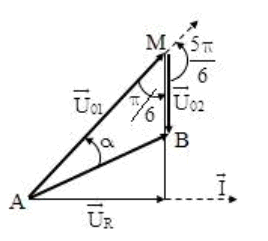
Độ lệch pha giữa \({{\overrightarrow{U}}_{01}}\) và \({{\overrightarrow{U}}_{02}}\) là \(\frac{\pi }{3}+\frac{\pi }{2}=\frac{5\pi }{6}\)
Áp dụng định lý hàm sin trong tam giác AMB:
\(\frac{{{U}_{0}}}{\sin \frac{\pi }{6}}=\frac{{{U}_{01}}}{\underbrace{\sin \left( \pi -\frac{\pi }{6}-\alpha \right)}_{\sin \left( \frac{\pi }{6}+\alpha \right)}}=\frac{{{U}_{02}}}{\sin \alpha }\)
Áp dụng chất dãy tỉ số bằng nhau:
\(\frac{{{U}_{0}}}{\sin \frac{\pi }{6}}=\frac{{{U}_{01}}+{{U}_{02}}}{\sin \left( \frac{\pi }{6}+\alpha \right)+\sin \alpha }\Rightarrow {{U}_{01}}+{{U}_{02}}=\frac{2{{U}_{0}}\cos \frac{\pi }{12}}{\sin \frac{\pi }{6}}.\sin \left( \frac{\pi }{12}+\alpha \right)\)
\(\Rightarrow {{\left( {{U}_{01}}+{{U}_{02}} \right)}_{\max }}=\frac{2{{U}_{0}}\cos \frac{\pi }{12}}{\sin \frac{\pi }{6}}\approx 1202V\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Yên Dũng
Copyright © 2021 HOCTAP247
