Hai nguồn phát sóng kết hợp tại A, B trên mặt nước cách nhau 12cm

* Hướng dẫn giải

Bước sóng: \(\lambda =\frac{v}{f}=\frac{32}{20}=1,6cm\)

Xét tỷ số: \(\frac{{{d}_{2}}-{{d}_{1}}}{\lambda }=\frac{9-4,2}{1,6}=3\)

Vậy ban đầu M nằm trên cực đại bậc 3.

Dịch chuyển B ra xa một đoạn \(\Delta d\), để đoạn này là nhỏ nhất thì khi đó M phải nằm trên cực tiểu thứ 4 với:

\({{d}_{2}}^{\prime }-{{d}_{1}}=\left( 3+\frac{1}{2} \right)\lambda =3,5\lambda =3,5.1,6=5,6cm\Rightarrow {{d}_{2}}^{\prime }=9,8cm\)

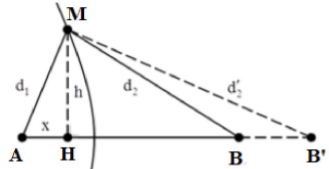
Áp dụng định lí hàm số cos cho tam giác MAB ta có:

\(M{{B}^{2}}=M{{A}^{2}}+A{{B}^{2}}-2AM.AB.cosA\)

\(\Rightarrow cosA=\frac{M{{A}^{2}}+A{{B}^{2}}-M{{B}^{2}}}{2AM.AB}=\frac{4,{{2}^{2}}+{{12}^{2}}-{{9}^{2}}}{2.4,2.12}=0,8\)

\(\Rightarrow \left\{ \begin{align} & AH=AM.cosA=4,2.0,8=3,36cm \\ & MH=AM.\sin A=4,2.0,6=2,52cm \\ \end{align} \right.\)

Áp dụng định lý Pitago trong tam giác vuông MHB’ ta có:

\(H{B}'=\sqrt{M{{{{B}'}}^{2}}-M{{H}^{2}}}=\sqrt{9,{{8}^{2}}-2,{{52}^{2}}}=9,47cm\)

Đoạn dịch chuyển:

\(B{B}'=H{B}'-HB=H{B}'-\left( AB-AH \right)=9,47-\left( 12-3,36 \right)=0,83cm\)