Một con lắc lò xo dao động điều hòa theo phương trình \(x=A\cos \omega t\)

* Hướng dẫn giải

Từ phương trình dao động, ta thấy pha ban đầu là 0

Động năng của vật bằng \(\frac{3}{4}\) năng lượng dao động, ta có:

\({{W}_{d}}=\frac{3}{4}W\Rightarrow {{W}_{t}}=\frac{1}{4}W\Rightarrow \frac{1}{2}k{{x}^{2}}=\frac{1}{4}.\frac{1}{2}k{{A}^{2}}\)

\(\Rightarrow {{x}^{2}}=\frac{1}{4}{{A}^{2}}\Rightarrow x=\pm \frac{A}{2}\)

Ta có VTLG:

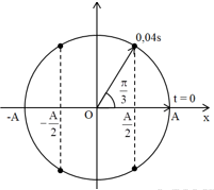
Từ VTLG, ta thấy khi vật qua li độ \(x=\frac{A}{2}\) lần đầu tiên, vecto quay được góc: \(\Delta \varphi =\frac{\pi }{3}\left( rad \right)\)

Tần số góc: \(\omega =\frac{\Delta \varphi }{\Delta t}=\frac{\frac{\pi }{3}}{0,04}=\frac{25\pi }{3}\left( rad/s \right)\)

\(\Rightarrow T=\frac{2\pi }{\omega }=\frac{2\pi }{\frac{25\pi }{3}}=0,24\left( s \right)\)

Động năng của vật biến thiên với chu kì: \({T}'=\frac{T}{2}=0,12\left( s \right)\)