Một vật dao động điều hòa trên quỹ đạo dài 20cm.

* Hướng dẫn giải

Biên độ dao động là: \(A=\frac{L}{2}=\frac{20}{2}=10\left( cm \right)\)

Vật đi được 10cm thì tới vị trí có \(x=5cm\) và chưa đổi chiều → ban đầu vật ở li độ \({{x}_{0}}=-5cm\) và đang đi theo chiều dương.

Ta có VTLG:

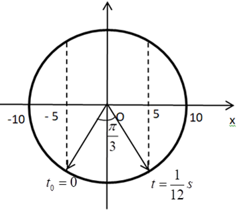
Từ VTLG, ta thấy pha ban đầu của dao động là: \(\varphi =-\frac{2\pi }{3}rad\)

Sau \(\frac{1}{12}s\) kể từ thời điểm ban đầu, vật đi từ li độ \({{x}_{0}}=-5cm\) tới \(x=5cm\), góc quét được là \(\Delta \varphi =\frac{\pi }{3}\).

\(\Rightarrow \omega =\frac{\Delta \varphi }{\Delta t}=\frac{\frac{\pi }{3}}{\frac{1}{12}}=4\pi \left( rad/s \right)\)

Vậy phương trình dao động của vật là: \(x=10\cos \left( 4\pi t-\frac{2\pi }{3} \right)cm\)