Một sóng hình sin đang truyền trên một sợi dây theo chiều dương của trục Ox

* Hướng dẫn giải

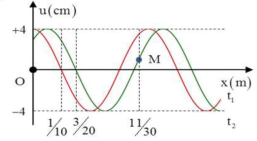
Từ đồ thị ta thấy: \(\frac{\lambda }{4}=\frac{1}{10}\Rightarrow \lambda =0,4m=40~\text{cm}\)

Trong thời gian ly pha dao động truyền được: \(\frac{3}{20}-\frac{1}{10}=0,05m=5~\text{cm}=\frac{\lambda }{8}\Rightarrow \text{ Chu k }\!\!\grave{\mathrm{i}}\!\!\text{ : }T=8s\)

\(\Rightarrow \) Vận tốc sóng: \(v=\frac{\lambda }{T}=\frac{40}{8}=5~\text{cm}/\text{s}\)

Độ lệch pha dao động của M và O là: \(\Delta \varphi =\frac{2\pi x}{\lambda }=\frac{2\pi \frac{11}{30}}{0,4}=\frac{11\pi }{6}\)

Tại t₁, M chuyển động theo chiều âm do nằm trước đỉnh sóng. 

Hai thời điểm \({{t}_{1}}\text{ v }\!\!\grave{\mathrm{a}}\!\!\text{  }{{t}_{2}}\) lệch nhau \(\frac{1}{8}\) chu kì, ứng với góc \(\frac{\pi }{4}\)

Tốc độ của M tại thời điểm t₂ là: \(v=-{{v}_{\max }}\cdot \cos \left( {{15}^{0}} \right)\approx -3,029~\text{cm}/\text{s}\)