Hai con lắc lò xo giống nhau có cùng khối lượng vật nặng m và cùng độ cứng
Câu hỏi :
Hai con lắc lò xo giống nhau có cùng khối lượng vật nặng m và cùng độ cứng lò xo k. Hai con lắc dao động trên hai đường thẳng song song, có vị trí cân bằng ở cùng gốc tọa độ. Chọn mốc thế năng tại vị trí cân bằng, đồ thị li độ - thời gian của hai dao động được cho như hình vẽ (con lắc thứ hai có biên độ nhỏ hơn con lắc thứ nhất ). Ở thời điểm t, con lắc thứ nhất có vận tốc 72cm/s và con lắc thứ hai có thế năng \({{4.10}^{-3}}J.\) Lấy \({{\pi }^{2}}=10.\) Khối lượng m là: 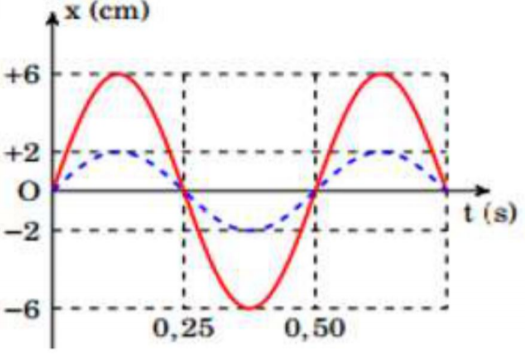
A. \(2\text{kg}\)
B. \(\frac{2}{9}kg\)
C. \(\frac{1}{3}kg\)
D. \(\frac{5}{4}kg\)
* Đáp án
D
* Hướng dẫn giải
Từ đồ thị ta có:
+ Chu kì: \(T=0,5s\Rightarrow \omega =\frac{2\pi }{T}=4\pi (ra\text{d/s)}\)
+ Biên độ dao động: \({{A}_{1}}=6cm;{{A}_{2}}=2cm\)
\(\Rightarrow \) Phương trình dao động của hai con lắc lò xo:
\(\left\{ \begin{array}{*{35}{l}} {{x}_{1}}=6.\cos \left( 4\pi t-\frac{\pi }{2} \right)cm \\ {{x}_{2}}=2.\cos \left( 4\pi t-\frac{\pi }{2} \right)cm \\ \end{array} \right.\)
\(\Rightarrow \frac{{{x}_{1}}}{{{x}_{2}}}=\frac{{{A}_{1}}}{{{A}_{2}}}=3\Rightarrow \frac{{{W}_{t1}}}{{{W}_{t2}}}=\frac{x_{1}^{2}}{x_{2}^{2}}=\frac{A_{1}^{2}}{A_{2}^{2}}=9\)
Ở thời điểm t ta có: \(\frac{{{W}_{t1}}}{{{W}_{t2}}}=\frac{{{W}_{1}}-{{W}_{d1}}}{{{W}_{t2}}}=9\Leftrightarrow \frac{\frac{1}{2}m.{{\omega }^{2}}A_{1}^{2}-\frac{1}{2}mv_{1}^{2}}{{{W}_{t2}}}=9\)
\(\Leftrightarrow \frac{\frac{1}{2}.m.{{(4\pi )}^{2}}.0,{{06}^{2}}-\frac{1}{2}.m.0,{{72}^{2}}}{{{4.10}^{-3}}}=9\Rightarrow m=1,25kg=\frac{5}{4}kg\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Chuyên Nguyễn Bỉnh Khiêm - Quảng Nam
Copyright © 2021 HOCTAP247
