Trên mặt nước có hai nguồn sóng kết hợp dao động đồng pha tại A, B.
Câu hỏi :
Trên mặt nước có hai nguồn sóng kết hợp dao động đồng pha tại A, B. Biết sóng lan truyền trên mặt nước với bước sóng \(\lambda \) và \(AB=5,6\lambda .\Delta \) là đường trung trực thuộc mặt nước của AB. M, N, P, Q là bốn điểm không thuộc \(\Delta ,\) dao động với biên độ cực đại, đồng pha với nguồn và gần \(\Delta \) nhất. Trong 4 điểm M, N, P, Q, khoảng cách giữa hai điểm xa nhau nhất có giá trị gần nhất với giá trị nào sau đây?
A. \(4,32\lambda \)
B. \(1,26\lambda \)
C. \(2,07\lambda \)
D. \(4,14\lambda \)
* Đáp án
A
* Hướng dẫn giải
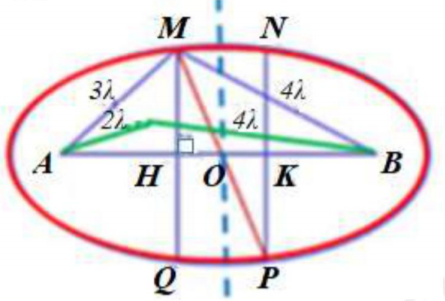
M, N, P, Q thuộc hình chữ nhật, khoảng cách gần nhất bằng độ dài đoạn MN, khoảng cách giữa hai điểm xa nhau nhất bằng độ dài đoạn MP. Ta xét điểm M.
* M dao động với biên độ cực đại: \({{d}_{2}}-{{d}_{1}}=k\lambda \)
* M dao động cùng pha với nguồn:
+ TH1: \(\left\{ \begin{array}{*{35}{l}} {{d}_{2}}-{{d}_{1}}={{k}_{le}}\lambda \\ {{d}_{2}}+{{d}_{1}}={{n}_{le}}\lambda >5,4\lambda \\ \end{array} \right.\)
+ TH2: \(\left\{ \begin{array}{*{35}{l}} {{d}_{2}}-{{d}_{1}}={{k}_{chan~}}\lambda \\ {{d}_{2}}+{{d}_{1}}={{n}_{chan~}}\lambda >5,4\lambda \\ \end{array} \right.\)
* M gần \(\Delta \) nhất thì
+ TH1: \(\left\{ \begin{array}{*{35}{l}} {{d}_{2}}-{{d}_{1}}=1.\lambda \\ {{d}_{2}}+{{d}_{1}}=7\lambda \\ \end{array}\Rightarrow \left\{ \begin{array}{*{35}{l}} {{d}_{1}}=3\lambda =AM \\ {{d}_{2}}=4\lambda =BM \\ \end{array} \right. \right.\)
+ TH2: \(\left\{ \begin{array}{*{35}{l}} {{d}_{2}}-{{d}_{1}}=2.\lambda \\ {{d}_{2}}+{{d}_{1}}=6\lambda \\ \end{array}\Rightarrow \left\{ \begin{array}{*{35}{l}} {{d}_{1}}=2\lambda \\ {{d}_{2}}=4\lambda \\ \end{array} \right. \right.\) (loại)
Từ hình vẽ ta có: \(AH+HB=AB\)
\(\Leftrightarrow \sqrt{A{{M}^{2}}-M{{H}^{2}}}+\sqrt{B{{M}^{2}}-M{{H}^{2}}}=AB\)
\(\Leftrightarrow \sqrt{{{(3\lambda )}^{2}}-M{{H}^{2}}}+\sqrt{{{(4\lambda )}^{2}}-M{{H}^{2}}}=5,4\lambda \)
\(\Rightarrow MH=2,189\lambda \Rightarrow AH=\sqrt{A{{M}^{2}}-M{{H}^{2}}}=2,051\lambda \)
\(\Rightarrow HO=AO-AH=\frac{5,4\lambda }{2}-2,051\lambda =0,649\lambda \)
\(\Rightarrow OM=\sqrt{M{{H}^{2}}+O{{H}^{2}}}=2,283\lambda \)
Khoảng cách giữa hai điểm xa nhau nhất có giá trị bằng: \(MP=2.OM=2.2,283\lambda =4,566\lambda \)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Chuyên Nguyễn Bỉnh Khiêm - Quảng Nam
Copyright © 2021 HOCTAP247
