Một sóng ngang truyền trên sợi dây đủ dài với bước sóng 60 cm.
Câu hỏi :
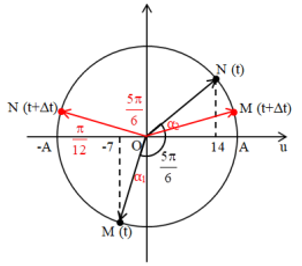
Một sóng ngang truyền trên sợi dây đủ dài với bước sóng 60 cm. Khi chưa có sóng truyền qua, gọi M và N là hai điểm gắn với hai phần tử trên dây cách nhau 85 cm. Hình bên là hình vẽ mô tả hình dạng sợi dây khi có sóng truyền qua ở thời điểm t, trong đó điểm M đang dao động về vị trí cân bằng. Coi biên độ sóng không đổi trong quá trình truyền sóng. Gọi t + ∆t là thời điểm gần t nhất mà khoảng cách giữa M và N đạt giá trị lớn nhất (với ∆t > 0). Diện tích hình thang tạo bởi M, N ở thời điểm t và M, N thời điểm t + ∆t gần nhất với kết quả nào sau đây? 
A. 2230 cm2.
B. 2560 cm2.
C. 2165 cm2.
D. 2315 cm2.
* Đáp án
D
* Hướng dẫn giải
Tại thời điểm t, điểm M đang đi lên → sóng truyền từ N tới M
→ Điểm N sớm pha hơn điểm M → điểm N đang đi xuống
Độ lệch pha giữa hai điểm M, N là:
\(\Delta \varphi =\frac{2\pi d}{\lambda }=\frac{2\pi .85}{60}=\frac{17\pi }{6}=2\pi +\frac{5\pi }{6}(\text{rad})\)
Hai điểm M, N có khoảng cách lớn nhất khi chúng đối xứng qua trục Oy Ta có vòng tròn lượng giác:
Từ vòng tròn lượng giác ta thấy:
\({{\alpha }_{1}}+{{\alpha }_{2}}=\frac{5\pi }{6}-\frac{\pi }{2}=\frac{2\pi }{3}(\text{rad})\)
\(\Rightarrow \arcsin \frac{7}{A}+\arccos \frac{14}{A}=\frac{2\pi }{3}\Rightarrow A\approx 17,35(~\text{cm})\)
Ở thời điểm t + ∆t, hai điểm M, N đối xứng qua trục Oy, ta có:
\(\left\{ \begin{array}{*{35}{l}} {{x}_{2N}}=A\cos \left( \frac{\pi }{12}+\frac{5\pi }{6} \right)\approx -16,76(~\text{cm}) \\ {{x}_{2M}}=A\cos \frac{\pi }{12}\approx 16,76(~\text{cm}) \\ \end{array} \right.\)
Diện tích hình thang tạo bởi M, N ở thời điểm t và M, N thời điểm t + ∆t là:
\(S=\frac{\left( \left| {{x}_{2M}}-{{x}_{1M}} \right|+\left| {{x}_{2N}}-{{x}_{1N}} \right| \right)\cdot d}{2}=\frac{(|16,76-(-7)|+|-16,76-14|)\cdot 85}{2}=2317,1\left( ~\text{c}{{\text{m}}^{2}} \right)\)
Diện tích S có giá trị gần nhất là 2315 cm2
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Chuyên ĐH Sư Phạm - Lần 1
Copyright © 2021 HOCTAP247