Một điểm sáng đặt tại điểm O trên trục chính của một thấu kính hội tụ
Câu hỏi :
Một điểm sáng đặt tại điểm O trên trục chính của một thấu kính hội tụ (O không là quang tâm của thấu kính). Xét trục Ox vuông góc với trục chính của thấu kính với O là gốc toạ độ như hình vẽ. Tại thời điểm t = 0, điểm sáng bắt đầu dao động điều hoà dọc theo trục Ox theo phương trình \(x=A\cos \left( 2\pi t-\frac{\pi }{2} \right)(\text{cm}),\) trong đó t tính bằng s. Trong khoảng thời gian \(\frac{13}{12}s\) kể từ thời điểm t = 0, điểm sáng đi được quãng đường là 18 cm. Cũng trong khoảng thời gian đó, ảnh của điểm sáng đi được quãng đường là 36 cm. Biết trong quá trình dao động, điểm sáng và ảnh của nó luôn có vận tốc ngược hướng nhau. Khoảng cách lớn nhất giữa điểm sáng và ảnh của nó trong quá trình dao động là 37 cm. Tiêu cự của thấu kính có giá trị gần nhất với giá trị nào trong các giá trị sau? .png)
A. 8,9 cm.
B. 12,1 cm.
C. 7,9 cm.
D. 10,1 cm.
* Đáp án
C
* Hướng dẫn giải
Nhận xét: ảnh luôn có vận tốc ngược hướng với điểm sáng → ảnh dao động ngược pha với điểm sáng
→ ảnh là ảnh thật
Từ phương trình chuyển động, ta thấy pha ban đầu của điểm sáng S là \(-\frac{\pi }{2}\text{rad}\)
→ pha ban đầu của ảnh S’ là \(\frac{\pi }{2}\text{rad}\)
Trong khoảng thời gian \(\frac{13}{12}s\) vecto quét được góc là:
\(\Delta \varphi =\omega \Delta t=2\pi \cdot \frac{13}{12}=\frac{13\pi }{6}=2\pi +\frac{\pi }{6}(\text{rad})\)
Ta có vòng tròn lượng giác:
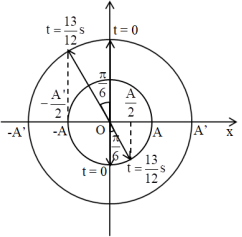
Từ vòng tròn lượng giác, ta thấy quãng đường điểm sáng S’ và ảnh S’ đi được trong thời gian \(\frac{13}{12}s\) là:
\(\left\{ \begin{array}{*{35}{l}} 4A+\frac{A}{2}=18(cm)\Rightarrow A=4(~\text{cm}) \\ 4{{A}^{\prime }}+\frac{{{A}^{\prime }}}{2}=36(~\text{cm})\Rightarrow {{A}^{\prime }}=8(~\text{cm}) \\ \end{array}\Rightarrow \frac{{{x}^{\prime }}}{x}=-\frac{{{A}^{\prime }}}{A}=-2\Rightarrow {{x}^{\prime }}=-2x \right.\)
Độ phóng đại của ảnh là:
\(|k|=\left| -\frac{{{d}^{\prime }}}{d} \right|=\frac{{{A}^{\prime }}}{A}\Rightarrow \frac{{{d}^{\prime }}}{d}=\frac{{{A}^{\prime }}}{A}=2\Rightarrow {{d}^{\prime }}=2d\)
Khoảng cách giữa ảnh và vật theo phương dao động là:
\(\Delta x=\left| x-{{x}^{\prime }} \right|=|3x|\Rightarrow \Delta {{x}_{\max }}=3A=12(~\text{cm})\)
Khoảng cách lớn nhất giữa ảnh và vật là:
\({{D}_{\max }}=\sqrt{{{(\Delta x)}^{2}}+{{\left( d+{{d}^{\prime }} \right)}^{2}}}\Rightarrow 37=\sqrt{{{12}^{2}}+{{\left( d+{{d}^{\prime }} \right)}^{2}}}\Rightarrow d+{{d}^{\prime }}=35(~\text{cm})\)
\(\Rightarrow \left\{ \begin{array}{*{35}{l}} d=\frac{35}{3}(~\text{cm}) \\ {{d}^{\prime }}=\frac{70}{3}(~\text{cm}) \\ \end{array} \right.\)
Áp dụng công thức thấu kính, ta có:
\(\frac{1}{d}+\frac{1}{{{d}^{\prime }}}=\frac{1}{f}\Rightarrow \frac{3}{35}+\frac{3}{70}=\frac{1}{f}\Rightarrow f=\frac{90}{7}\approx 7,78(~\text{cm})\)
Tiêu cự của thấu kính gần nhất với giá trị 7,9 cm
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Chuyên ĐH Sư Phạm - Lần 1
Copyright © 2021 HOCTAP247
