Cho hình hộp chữ nhật ABCD.A'B'C'D'. Chứng minh

* Hướng dẫn giải

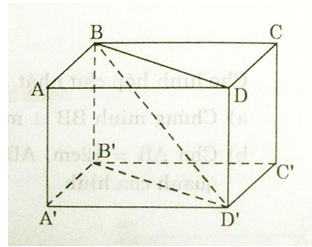
a) Ta có ABB’A’ là hình chữ nhật nên: AA’ // BB’ và AA’ = BB’

Tương tự ADD’A’ là hình chữ nhật:

AA’ // DD’ và AA’ = DD’

=> BB’ // DD’ và BB’ = DD’

Do đó BB’D’D là hình bình hành

=>BD // B’D’

b) BB’C’C là hình chữ nhật: BB’ // CC’ mà BB’ không thuộc mp(CC’D’D) và CC’ thuộc mp(CC’D’D) nên BB’ // mp(CC’D’D)

B’D’ // BD (cmt) mà B’D’ không thuộc mp (ABCD) và BD thuộc mp(ABCD) nên B’D’ // mp(ABCD)

c) Ta có: AB // CD (ABCD là hình chữ nhật)

AA’ // DD’ (ADD’A’ là hình chữ nhật)

Mà mp(ABB’A’) chứa hai đường thẳng cắt nhau AB và AA’ và mp(DCC’D’) chứa hai đường thẳng cắt nhau CD và DD’ => mp(ABB’A’) // mp(DCC’D’)