1 vật thực hiện đồng thời 2 dao động điều hòa cùng phương cùng tần số

* Hướng dẫn giải

Dao động tổng hợp: \(x={{x}_{1}}+{{x}_{2}}=2\angle -\frac{\pi }{3}+2\angle 0=2\sqrt{3}\angle -\frac{\pi }{6}\Rightarrow x=2\sqrt{3}\cos \left( 2\pi t-\frac{\pi }{6} \right)cm\).

Tại thời điểm ban đầu: \(\left\{ \begin{align} & {{x}_{0}}=2\sqrt{3}\cos \left( -\frac{\pi }{6} \right)=\frac{A\sqrt{3}}{2} \\ & {{v}_{0}}=-A\omega \sin \left( -\frac{\pi }{6} \right)>0 \\ \end{align} \right.\)

Tại vị trí có \({{W}_{\mathsf{}}}={{W}_{t}}\Rightarrow x=\pm \frac{A}{\sqrt{2}}\).

Vẽ trên trục thời gian, ta được:

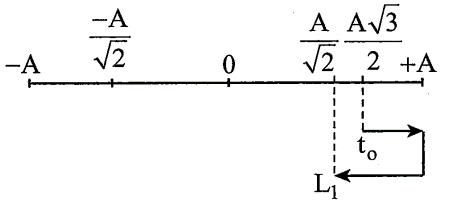
Quãng đường vật đi được trong thời gian đó: \(S=\left( A-\frac{A\sqrt{3}}{2} \right)+\left( A-\frac{A}{\sqrt{2}} \right)=4\sqrt{3}-3-\sqrt{6}\left( cm \right)\).

Thời gian vật đi được khi đó: \(\Delta t=\frac{T}{12}+\frac{T}{8}=\frac{5T}{24}=\frac{5}{24}s\).

Tốc độ trung bình của vật trong khoảng thời gian đó: \({{v}_{tb}}=\frac{S}{t}=\frac{4\sqrt{3}-3-\sqrt{6}}{\frac{5}{24}}=7,0978\ cm/s\).