Hai chất điểm M, N dđ điều hòa trên các quỹ đạo song song, gần nhau dọc theo trục Ox
Câu hỏi :
Hai chất điểm M, N dao động điều hòa trên các quỹ đạo song song, gần nhau dọc theo trục Ox, có li độ lần lượt là \({{x}_{1}}\) và \({{x}_{2}}\). Hình bên là đồ thị biểu diễn sự phụ thuộc của \({{x}_{1}}\) và \({{x}_{2}}\) theo thời gian t. Trong quá trình dao động, khoảng cách lớn nhất giữa hai chất điểm xét theo phương Ox là: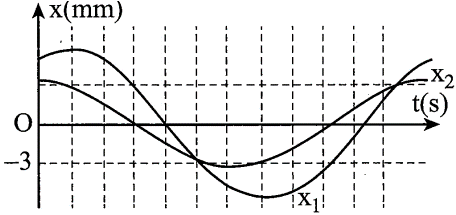
A. 4,5 mm.
B. 5,5 mm.
C. 2,5 mm.
D. 3,5 mm.
* Đáp án
D
* Hướng dẫn giải
Từ đồ thị ta thấy:
Chu kì \(T=12\) đơn vị thời gian.
\({{x}_{1}}\) trễ pha hơn \({{x}_{2}}\) là: \(\frac{1}{12}.2\pi =\frac{\pi }{6}\).
Khoảng cách giữa \({{x}_{1}}\) và \({{x}_{2}}\) theo phương Ox là: \(x={{x}_{1}}-{{x}_{2}}=A\cos \left( \omega t+\varphi \right)\).
\(\Rightarrow \)Khoảng cách này lớn nhất bằng \({{X}_{\max }}=A=\sqrt{A_{1}^{2}+A_{2}^{2}-2{{A}_{1}}{{A}_{2}}.\cos \Delta \varphi }\).
Tại \(t=5\) đơn vị thời gian thì cả hai vật đều có li độ là \(-3cm\).
Ban đầu \({{x}_{2}}\) cực đại, nên pha ban đầu của \({{x}_{2}}\) là: \({{\varphi }_{02}}=0\).
\({{x}_{2}}={{A}_{2}}\cos \left( \frac{2\pi }{12}.5+0 \right)=-3\Rightarrow {{A}_{2}}=2\sqrt{3}cm\).
Từ vị trí ban đầu của \({{x}_{1}}\) xác định được pha ban đầu của là: \({{\varphi }_{01}}=-\frac{1}{12}.2\pi =-\frac{\pi }{6}\).
\({{x}_{1}}={{A}_{1}}\cos \left( \frac{2\pi }{12}.5-\frac{\pi }{6} \right)=-3\Rightarrow {{A}_{1}}=6cm\).
Khoảng cách giữa \({{x}_{1}}\) và \({{x}_{2}}\) lớn nhất bằng:
\({{X}_{\max }}=A=\sqrt{A_{1}^{2}+A_{2}^{2}-2{{A}_{1}}{{A}_{2}}.\cos \Delta \varphi }=\sqrt{{{6}^{2}}+{{\left( 2\sqrt{3} \right)}^{2}}-2.6.2\sqrt{3}.\cos \frac{\pi }{6}}=3,464cm\).
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Võ Văn Kiệt
Copyright © 2021 HOCTAP247
