Trên mặt nước nằm ngang tại hai điểm A và B người ta đặt hai nguồn kết hợp
Câu hỏi :
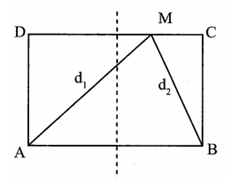
Trên mặt nước nằm ngang tại hai điểm A và B người ta đặt hai nguồn kết hợp dao động cùng pha theo phương thẳng đứng. Hình chữ nhật ABCD nằm trên mặt nước sao cho \(\frac{AD}{AB}=\frac{3}{4}\) . Biết rằng trên CD có 7 điểm dao động với biên độ cực đại. Trên AB có tối đa bao nhiêu điểm dao động với biên độ cực đại?
A. 5
B. 9
C. 11
D. 13
* Đáp án
C
* Hướng dẫn giải
Ta có: \(\left\{ \begin{align} & AB=a \\ & \frac{AD}{AB}=\frac{3}{4}\Rightarrow AD=CB=\frac{3}{4}a \\ \end{align} \right.\)
\(\Rightarrow DB=CA=\sqrt{A{{B}^{2}}+A{{D}^{2}}}=\sqrt{{{a}^{2}}+{{\left( \frac{3}{4}a \right)}^{2}}}=\frac{5a}{4}\)
Số cực đại trên đoạn CD bằng số giá trị k nguyên thỏa mãn:
\(\frac{CB-CA}{\lambda }\le k\le \frac{DB-DA}{\lambda }\)
Trên CD có 7 điểm dao động với biên độ cực đại nên:
\(k\le 3\Leftrightarrow \frac{DB-DA}{\lambda }\le 3\Leftrightarrow \frac{\frac{5a}{4}-\frac{3a}{4}}{\lambda }\le 3\Leftrightarrow \frac{a}{\lambda }\le 6\left( 1 \right)\)
Số cực đại trên đoạn AB bằng số giá trị k’ nguyên thỏa mãn:
\(-\frac{AB}{\lambda }<k'<\frac{AB}{\lambda }\Leftrightarrow -\frac{a}{\lambda }<k'<\frac{a}{\lambda }\left( 2 \right)\)
Từ (1) và (2) \(\to k'<6\)
\(\to \) Trên AB có tối đa 11 điểm dao động với biên độ cực đại (ứng với \(k'=0;\pm 1;\pm 2;\pm 3;\pm 4;\pm 5)\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Nguyễn Trung Trực
Copyright © 2021 HOCTAP247