Dùng hạt\(\alpha \) có động năng K bắn vào hạt nhân\(_{7}^{14}N\) đứng yên
Câu hỏi :
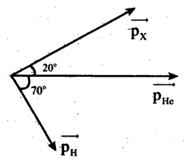
Dùng hạt \(\alpha \) có động năng K bắn vào hạt nhân \(_{7}^{14}N\) đứng yên gây ra phản ứng: \(_{2}^{4}He+_{7}^{14}N\to X+_{1}^{1}H\) . Phản ứng này thu được năng lượng 1,21MeV và không kèm theo bức xạ gam-ma. Lấy khối lượng các hạt nhân tính theo đơn vị u bằng số khối của chúng. Hạt nhân X và hạt nhân \(_{1}^{1}H\) bay ra theo các hướng hợp với hướng chuyển động của hạt \(\alpha \) các góc lần lượt \({{20}^{o}}\) và \({{70}^{o}}\) . Động năng của hạt nhân \(_{1}^{1}H\) là
A. 0,775MeV.
B. 1,75 MeV.
C. 3,89 MeV.
D. 1,27 MeV.
* Đáp án
B
* Hướng dẫn giải
Áp dụng định luật bảo toàn năng lượng toàn phần: \(Q={{K}_{X}}+{{K}_{H}}-{{K}_{\alpha }}=-1,21MeV\)
Áp dụng định luật bảo toàn động lượng: \(\overrightarrow{{{P}_{\alpha }}}=\overrightarrow{{{P}_{X}}}+\overrightarrow{{{P}_{H}}}\)
Ta có, góc tạo bởi \(\overrightarrow{{{P}_{X}}}\bot \overrightarrow{{{P}_{H}}}\) nên:
|
\(\begin{array}{l} \tan {20^o} = \frac{{{P_H}}}{{{P_X}}} \Leftrightarrow {\left( {\tan {{20}^o}} \right)^2} = \frac{{{m_H}{K_H}}}{{{m_X}{K_X}}}\\ \to {K_X} = \frac{{{m_H}{K_H}}}{{{m_X}{{\left( {\tan {{20}^o}} \right)}^2}}} = \frac{{{K_H}}}{{17{{\left( {\tan {{20}^o}} \right)}^2}}}\\ \sin {20^o} = \frac{{{P_H}}}{{{P_\alpha }}} \Leftrightarrow {\left( {\sin {{20}^o}} \right)^2} = \frac{{{m_H}{K_H}}}{{{m_\alpha }{K_\alpha }}}\\ \to {K_\alpha } = \frac{{{m_H}{K_H}}}{{{m_\alpha }{{\left( {\tan {{20}^o}} \right)}^2}}} = \frac{{{K_H}}}{{4{{\left( {\sin {{20}^o}} \right)}^2}}} \end{array}\) \(\frac{{{K}_{H}}}{17{{\left( \tan {{20}^{2}} \right)}^{2}}}+{{K}_{H}}-\frac{{{K}_{H}}}{4{{\left( \sin {{20}^{o}} \right)}^{2}}}=-1,21MeV\) suy ra \({{K}_{H}}=1,746MeV\) |
|
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi thử THPT QG năm 2021 môn Vật Lý Trường THPT Nguyễn Trung Trực
Copyright © 2021 HOCTAP247