Dùng hạt có động năng 5,00MeV bắn vào hạt nhân\(_{7}^{14}N\) đang đứng yên

* Hướng dẫn giải

+ Theo định luật bảo toàn năng lượng toàn phần:

\(Q={{K}_{H}}+{{K}_{X}}-{{K}_{He}}\to {{K}_{H}}+{{K}_{X}}=5-1,21=3,79\ MeV\to {{K}_{H}}=3,79-{{K}_{X}}\).

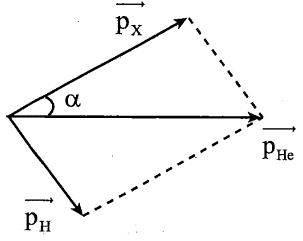
+ Áp dụng định luật bảo toàn vectơ động lượng: \(\overrightarrow{{{p}_{He}}}=\overrightarrow{{{p}_{H}}}+\overrightarrow{{{p}_{X}}}\)

\(\begin{array}{l}
\cos \alpha  = \frac{{p_{He}^2 + p_X^2 - p_H^2}}{{2{p_{He}}.{p_X}}} = \frac{{2{m_{He}}.{K_{He}} + 2{m_X}.{K_X} - 2{m_H}.{K_H}}}{{2\sqrt {2{m_{He}}.{K_{He}}} .\sqrt {2{m_X}.{K_X}} }}\\
\cos \alpha  = \frac{{4.5 + 17{K_X} - \left( {3,79 - {K_X}} \right)}}{{4\sqrt 5 .\sqrt {17{K_X}} }} = \frac{{16,21 + 18{K_X}}}{{4\sqrt {85} .\sqrt {{K_X}} }} = \frac{{\frac{{16,21}}{{\sqrt {{K_X}} }} + 18\sqrt {{K_X}} }}{{4\sqrt {85} }}
\end{array}\)

Áp dụng BĐT Cosi cho hệ thức \(\left( \frac{16,21}{\sqrt{{{K}_{X}}}}+18\sqrt{{{K}_{X}}} \right)\ge 2\sqrt{16,21.18}\). Nhận thấy \(\cos \alpha \) đạt min thì góc \(\alpha \) đạt max.

Dấu “=” xảy ra \(\Leftrightarrow \frac{16,21}{\sqrt{{{K}_{X}}}}=18\sqrt{{{K}_{X}}}\Rightarrow {{K}_{X}}=0,9006\ MeV\).