Trang chủ
Đề thi & kiểm tra
Lớp 12
Vật lý
Đề thi THPT QG năm 2021 môn Vật lý Bộ GD&ĐT- Mã đề 213
Đặt điện áp \(u=60\sqrt{2}\cos \left( 300t+\frac{\pi }{3} \right)\
Đặt điện áp \(u=60\sqrt{2}\cos \left( 300t+\frac{\pi }{3} \right)\
Câu hỏi :
Đặt điện áp \(u=60\sqrt{2}\cos \left( 300t+\frac{\pi }{3} \right)\,\left( V \right)\) vào hai đầu mạch AB như hình bên, trong đó R = 190 W và điện dung C của tụ điện thay đổi được. Khi C = C1 thì điện tích của bản tụ điện nối vào N là \(q=5\sqrt{2}{{.10}^{-4}}.\cos \left( 300t+\frac{\pi }{6} \right)\,\left( C \right)\). Trong các biểu thức, t tính bằng s. Khi C = C2 thì điện áp hiệu dụng giữa hai đầu R đạt giá trị cực đại, giá trị cực đại đó bằng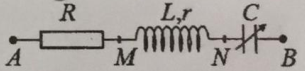
A. 60 V.
B. 29 V.
C. 57 V.
D. 81 V.
* Đáp án
C
* Hướng dẫn giải
Khi C = C1 thì:
I = Q.w = 5.10-4.300 = 0,15 A
\(\to Z=\frac{U}{I}=\frac{60}{0,15}=400\,\Omega \)
Do uC cùng pha với q ® uC chậm pha hơn so với u một góc là:
\(\frac{\pi }{3}-\frac{\pi }{6}=\frac{\pi }{6}\,rad\)
Theo hình vẽ, ta có tam giác ABH là một nửa của tam giác đều có đỉnh là B nên:
\(R+r=\frac{Z}{2}\to r=\frac{Z}{2}-R=\frac{400}{2}-190=10\,\Omega \)
Khi C = C2 thì URmax, tức là mạch xảy ra hiện tượng cộng hưởng:
UR + Ur = U = 60 V
\(\frac{{{U}_{R}}}{190}=\frac{{{U}_{r}}}{10}=\frac{{{U}_{R}}+{{U}_{r}}}{190+10}=\frac{U}{200}\)
\(\to {{U}_{R}}=\frac{190.U}{200}=\frac{190.60}{200}=57\,V\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi THPT QG năm 2021 môn Vật lý Bộ GD&ĐT- Mã đề 213
Số câu hỏi: 40
Copyright © 2021 HOCTAP247

