Hai con lắc lò xo giống hệt nhau được gắn vào điểm G của một giá cố định
Câu hỏi :
Hai con lắc lò xo giống hệt nhau được gắn vào điểm G của một giá cố định như hình bên. Trên phương nằm ngang và phương thẳng đứng, các con lắc đang dao động điều hòa với cùng biên độ 12 cm, cùng chu kì T nhưng vuông pha với nhau. Gọi FG là độ lớn hợp lực của các lực do hai lò xo tác dụng lên giá. Biết khoảng thời gian ngắn nhất giữa hai lần mà FG bằng trọng lượng của vật nhỏ của con lắc là \(\frac{T}{4}\). Lấy g = 10 m/s2. Giá trị của T gần nhất với giá trị nào sau đây?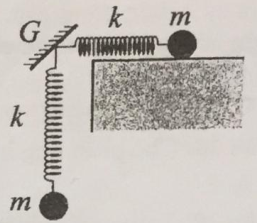
A. 0,68 s.
B. 0,52 s.
C. 0,57 s.
D. 0,63 s.
* Đáp án
C
* Hướng dẫn giải
Do hai lực lò xo vuông góc nhau nên:
\(\begin{align} & F_{G}^{2}=F_{1}^{2}+F_{2}^{2}={{\left( k{{x}_{1}}-mg \right)}^{2}}+{{\left( k{{x}_{2}} \right)}^{2}}={{\left( k{{x}_{1}} \right)}^{2}}-2.k{{x}_{1}}.mg+{{\left( mg \right)}^{2}}+{{\left( k{{x}_{2}} \right)}^{2}} \\ & ={{k}^{2}}\left( x_{1}^{2}+x_{2}^{2} \right)-2.k{{x}_{1}}.mg+{{\left( mg \right)}^{2}} \\ \end{align}\)
Do vuông pha nên: \(x_{1}^{2}+x_{2}^{2}={{A}^{2}}=0,{{12}^{2}}\)
Khi FG = P = mg thì: k2A2 = 2k.mg.x1 = 2k.mg.A.cos(wt + j)
=> \(\frac{m}{k}=\frac{A}{2g\cos \left( \omega t+\varphi \right)}\)
\(\Delta t=\frac{T}{4}\to \Delta \varphi =\omega .\Delta t=\frac{2\pi }{T}.\frac{T}{4}=\frac{\pi }{2}\)
\(\to \left( \omega t+\varphi \right)=\frac{\Delta \varphi }{2}=\frac{\pi }{4}\to \cos \left( \omega t+\varphi \right)=\frac{\sqrt{2}}{2}\)
=> \(\frac{m}{k}=\frac{A}{2g\cos \left( \omega t+\varphi \right)}=\frac{0,12}{2.10.\frac{\sqrt{2}}{2}}=6\sqrt{2}{{.10}^{-3}}\)
\(T=2\pi \sqrt{\frac{m}{k}}=2\pi \sqrt{6\sqrt{2}{{.10}^{-3}}}=0,579\,s\)
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Đề thi THPT QG năm 2021 môn Vật lý Bộ GD&ĐT- Mã đề 213
Copyright © 2021 HOCTAP247
