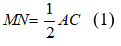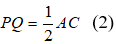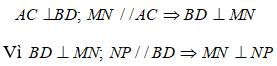Cho tứ giác ABCD có hai đường chéo AC và BD vuông góc với nhau

* Hướng dẫn giải

* Xét tam giác ABC có M và N lần lượt là trung điểm của AB và BC nên MN là đường trung bình của tam giác 

Suy ra: MN// AC và

* Xét tam giác ACD có P và Q lần lượt là trung điểm của CD và AD nên PQ là đường trung bình của tam giác

Suy ra: PQ // AC và

Từ (1) và (2) suy ra: MN// PQ và MN = PQ

Do đó, tứ giác MNPQ là hình bình hành.

* Xét tam giác BCD có P và N lần lượt là trung điểm của CD và CB nên PN là đường trung bình của tam giác

Suy ra: NP // BD 

* Ta có

Hình bình hành MNPQ có 1 góc vuông nên là hình chữ nhật.

Vì hai cạnh kề của hình chữ nhật MNPQ chưa chắc đã bằng nhau (không có dữ kiện liên quan) nên MNPQ không thể là hình vuông.

Chọn đáp án C