Bài 5 trang 82 SGK Toán 7 tập 1
Lý thuyết
Bài tập
Mục lục
Tóm tắt bài
Đề bài
a) Vẽ góc ABC có số đo bằng \(56^{\circ}.\)
b) Vẽ góc ABC' kề bù với góc ABC. Hỏi số đo của góc ABC'?
c) Vẽ góc C'BA' kề bù với góc ABC'. Tính số đo của góc C'BA'.
Hướng dẫn giải
b. Áp dụng định nghĩa hai góc kề bù.
c. Áp dụng tính chất hai góc đối đỉnh.
Lời giải chi tiết
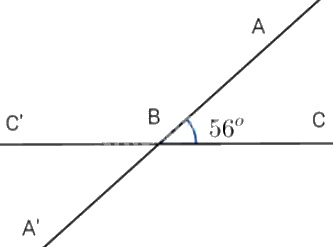
a) Trên hình vẽ bên, ta vẽ góc \(\widehat{ABC}=56^{\circ}\).
b) Vẽ tia đối của tia BC ta được tia BC', được góc ABC' kề bù với góc ABC.
Ta có \(\widehat{ABC'}=180^{\circ}-\widehat{ABC}=180^{\circ}-56^{\circ}\)\(=124^{\circ}\).
c) Vẽ tia đối của tia BA, ta được tia BA', thì góc C'BA' kề bù với góc ABC'.
Ta có \(\widehat{C'BA'}=\widehat{ABC}\) (hai góc đối đỉnh) nên \(\widehat{C'BA'}=56^{\circ}.\)
Copyright © 2021 HOCTAP247
