Đề kiểm tra 15 phút - Đề số 3 - Bài 1 - Chương 1 - Hình học 7

Đề bài

Hai đường thẳng AB và CD cắt nhau tại O sao cho góc \(\widehat {AOC} = {60^o}.\)

a) Tính số đo các góc còn lại.

b) Vẽ tia Ot là tia phân giác của \(\widehat {AOC}\)và Ot’ là tia đối của tia Ot. Chứng minh Ot’ là tia phân giác của góc \(\widehat {BOD}.\)

Hướng dẫn giải

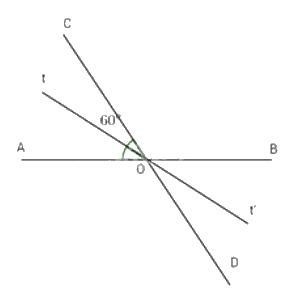
a) Ta có \( \Rightarrow \widehat {BOD} = \widehat {DOt} = {30^o}.\) \(\widehat {BOD} = \widehat {AOC} = {60^o}\)(đối đỉnh)

\(\widehat {AOC} + \widehat {COB} = {180^o}\)(kề bù)

\( \Rightarrow \widehat {COB} = {180^o} - \widehat {AOB}\)\(\;={180^o} - {60^o} = {120^o}\)

\(\widehat {AOD} = \widehat {COD} = {120^o}\)

b) Ot là tia phân giác của \(\widehat {AOC}\)nên

\(\widehat {AOt} = \widehat {COt} = \dfrac{1}{ 2}\widehat {AOC} = \dfrac {1 }{2}{.60^o} = {30^o}\)

Ot’ là tia đối của tia Ot nên \(\widehat {AOt}\) và \(\widehat {BOt'}\) là hai góc đối đỉnh

\( \Rightarrow \widehat {BOt'} = \widehat {AOt} = {30^o}\)

Tương tự \(\widehat {DOt'} = \widehat {COt} = {30^o}\)

\( \Rightarrow \widehat {BOt'} = \widehat {DOt} = {30^o}.\)

Do đó Ot’ là tia phân giác của góc \(\widehat {BOD}\).