Bài 6 trang 83 SGK Toán 7 tập 1
Lý thuyết
Bài tập
Mục lục
Tóm tắt bài
Đề bài
Vẽ hai đường thẳng cắt nhau sao cho trong các góc tạo thành có một góc \(47^{\circ}\). Tính số đo các góc còn lại.
Hướng dẫn giải
+ Vẽ hình.
+ Áp dụng định nghĩa và tính chất của hai góc đối đỉnh và hai góc kề bù.
Lời giải chi tiết
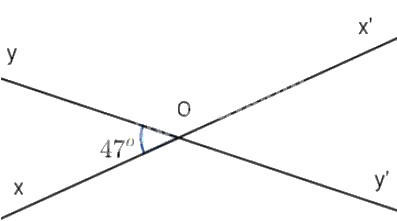
Giả sử hai đường thẳng xx' và yy' cắt nhau tại O và \(\widehat{xOy}=47^{\circ}\) (hình vẽ bên). Suy ra \(\widehat{x'Oy'}=\widehat{xOy}=47^{\circ}\) (hai góc đối đỉnh).
\(\widehat{xOy'}=180^{\circ}-\widehat{xOy}=180^{\circ}-47^{\circ}\)\(=133^{\circ}\) (do \(\widehat{xOy}\) và \(\widehat{xOy'}\) kề bù)
Và \(\widehat{x'Oy}=\widehat{xOy'}=133^{\circ}\) (hai góc đối đỉnh).
Copyright © 2021 HOCTAP247
