Đề kiểm tra 15 phút - Đề số 5 - Bài 1 - Chương 1 - Hình học 7

Đề bài

Bài 1: Cho hai góc kề \(\widehat {AOB}\) và \(\widehat {BOC}.\)

a) Hãy vẽ các góc \(\widehat {A'OB'}\) và \(\widehat {B'OC'}.\) Lần lượt đối đỉnh với \(\widehat {AOB}\) và \(\widehat {BOC}.\)

b) Cho \(\widehat {AOB} = {55^o},\) hãy tính số đo các góc \(\widehat {A'OB'}\) và \(\widehat {BOA'}.\)

Bài 2: . Cho hình vẽ bên.

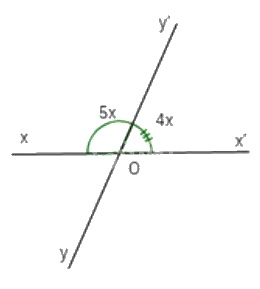
Hãy tính

 \(\widehat {xOy}\) và \(\widehat {yOx'}.\)

Hướng dẫn giải

Bài 1:  

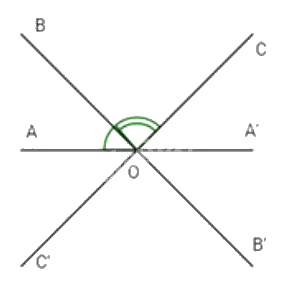
a) Góc đối đỉnh với góc \(\widehat {AOB}\) là \(\widehat {A'OB'}\) và góc đối đỉnh với góc \(\widehat {BOC}\) là góc \(\widehat {B'OC'}\).

b) Ta có \(\widehat {A'OB'} = \widehat {AOB} = {55^o}\)(đối đỉnh)

OA’ là tia đối của tia OA nên \(\widehat {AOB}\) và \(\widehat {BOA'}\) là hai góc kề bù.

Ta có:  \(\widehat {AOB} + \widehat {BOA'} = {180^o}\).

\( \Rightarrow \widehat {BOA'} = {180^o} - \widehat {AOB}\)\(\; = {180^o} - {55^o} = {125^o}.\)

Bài 2: Ta có Ox và Ox’ là hai tia đối nhau nên hay \(5x + 4x = {180^o} \Rightarrow 9x = {180^o}\)\(\; \Rightarrow x = {20^o}.\)

Vậy \(\widehat {xOy'} = {5.20^o} = {100^o};\)\(\,\,\widehat {y'{\rm{Ox}}'} = {4.20^o} = {80^o}\)

Ta có \(\widehat {xOy} = \widehat {x'Oy'} = {80^o}\)(đối đỉnh) và \(\widehat {yOx'} = \widehat {xOy'} = {100^o} \) (đối đỉnh)