Bài 44 trang 20 SGK Toán 8 tập 1
Tóm tắt bài
Đề bài
Phân tích các đa thức sau thành nhân tử:
a) x3 + \(\frac{1}{27}\); b) (a + b)3 – (a – b)3
c) (a + b)3 + (a – b)3 ; d) 8x3 + 12x2y + 6xy2 + y3
e) - x3 + 9x2 – 27x + 27.
Hướng dẫn giải
Áp dụng các hằng đẳng thức đáng nhớ: Tổng hai lập phương, hiệu hai lập phương.
Lời giải chi tiết
\(\begin{array}{l}
a)\,\,{x^3} + \frac{1}{{27}} = {x^3} + {\left( {\frac{1}{3}} \right)^3}\\
= \left( {x + \frac{1}{3}} \right)\left[ {{x^2} - \frac{1}{3}x + {{\left( {\frac{1}{3}} \right)}^2}} \right]\\ = \left( {x + \frac{1}{3}} \right)\left( {{x^2} - \frac{1}{3}x + \frac{1}{9}} \right)
\end{array}\)
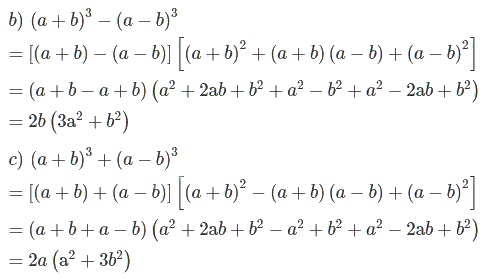
\(d)\,\,8{x^3} + 12{{\rm{x}}^2}y + 6{\rm{x}}{y^2} + {y^3}\\ = {\left( {2{\rm{x}}} \right)^3} + 3{\left( {2{\rm{x}}} \right)^2}.y + 3.2{\rm{x}}.{y^2} + {y^3}\\ = {\left( {2{\rm{x}} + y} \right)^3}\)
\(\begin{array}{l}
e)\; - {x^3} + 9{x^2} - 27x + 27 \\= 27 - 27x + 9{x^2} - {x^3}\\
= {3^3} - {3.3^2}x + 3.3{x^2} - {x^3}\\
= {\left( {3 - x} \right)^3}.
\end{array}\)
Copyright © 2021 HOCTAP247
