Trang chủ
Lớp 8
Toán Lớp 8 SGK Cũ
Bài 12. Chia đa thức một biến đã sắp xếp
Bài 74 trang 32 SGK Toán 8 tập 1
Bài 74 trang 32 SGK Toán 8 tập 1
Lý thuyết
Bài tập
Mục lục
Tóm tắt bài
Đề bài
Tìm số \(a\) để đa thức \(2{x^3} - 3{x^2} + x + a\) chia hết cho đa thức \(x + 2\).
Hướng dẫn giải
Áp dụng định lí: Một phép chia là phép chia hết thì số dư của phép chia phải bằng \(0\).
Lời giải chi tiết
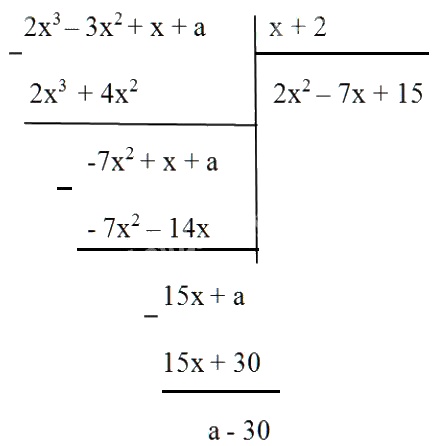
Ta có: \(2{x^3} - 3{x^2} + x + a \)\(= (2{x^2} - 7x + 15).(x + 2) + a - 30\)
Dư trong phép chia là \((a-30)\) để phép chia là phép chia hết thì dư của phép chia phải bằng \(0\) tức là:
\(a-30=0\Rightarrow a=30\)
Vậy \(a = 30\).
Copyright © 2021 HOCTAP247
