Bài 15 trang 119 SGK Toán 8 tập 1

Đề bài

Đố. Vẽ hình chữ nhật ABCD có AB = 5cm, BC = 3cm.

a) Hãy vẽ một hình chữ nhật có diện tích nhỏ hơn nhưng có chu vi lớn hơn hình chữ nhật ABCD. Vẽ được mấy hình như vậy.

b) Hãy vẽ hình vuông có chu vi bằng chu vi hình chữ nhật ABCD. Vẽ được mấy hình vuông như vậy? So sánh diện tích hình chữ nhật với diện tích hình vuông có cùng chu vi vừa vẽ. Tại sao trong các hình chữ nhật có cùng chu vi thì hình vuông có diện tích lớn nhất.

Hướng dẫn giải

Áp dụng công thức tính diện tích hình chữ nhật, diện tích hình vuông.

Lời giải chi tiết

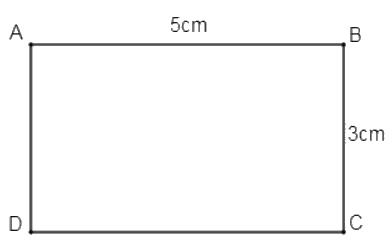
a) Hình chữ nhật ABCD đã cho có diện tích là S_ACBD = 3.5 = 15 (cm²).

- Hình chữ nhật có chiều rộng là 1cm, chiều dài là 12cm có diện tích là 12cm² và chu vi là ( 1+12).2 = 26(cm) (có 26>15).

- Hình chữ nhật có chiều rộng là 2cm, chiều dài là 7cm có diện tích là 14cm² và chu vi là (2+7).2 = 18(cm) (có 18 > 15).

Như vậy, vẽ được nhiều hình chữ nhật có diện tích bé hơn nhưng có chu vi lớn hơn hình chữ nhật  ABCD cho trước.

b) Chu vi hình chữ nhật ABCD đã cho là:

           (5+3).2 = 16 (cm)

Cạnh hình vuông có chu vi bằng chu vi hình chữ nhật ABCD là:

            16 : 4 = 4(cm).

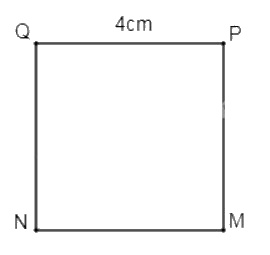
Diện tích hình vuông này là 4.4 = 16 (m²) 

Vẽ được một hình vuông như vậy.

+) Tổng quát:  Giả sử hình chữ nhật có các kích thước là \(a, b\). Khi đó:

- Diện tích của hình chữ nhật đó là: \(ab\)

- Cạnh của hình vuông có chu vi bằng chu vi hình chữ nhật là: \(\frac{{a + b}}{2}\)

Vậy diện tích hình vuông đó là: \({\left( {\frac{{a + b}}{2}} \right)^2}\)

Ta có: \({\left( {\frac{{a + b}}{2}} \right)^2} = \frac{{{{\left( {a + b} \right)}^2}}}{4} = \frac{{{a^2} + 2{\rm{a}}b + {b^2}}}{4}\)\( = \frac{{{{\left( {a - b} \right)}^2} + 4{\rm{a}}b}}{4} = \frac{{{{\left( {a - b} \right)}^2}}}{4} + ab \ge ab\)

( vì \(\frac{{{{\left( {a - b} \right)}^2}}}{4} \ge 0\,\forall \,a,\,b\))

Vậy trong các hình chữ nhật có cùng chu vi thì hình vuông có diện tích lớn nhất.