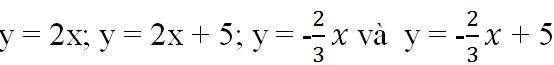Giải bài 15 trang 51 - Sách giáo khoa Toán 9 tập 1

Đề bài

   a) Vẽ đồ thị của các hàm số

trên cùng một mặt phẳng tọa độ.

 b) Bốn đường thẳng trên cắt nhau tạo thành tứ giác OABC (O là gốc tọa độ). Tứ giác OABC có phải là hình bình hành không? Vì sao ?

Hướng dẫn giải

     Hướng dẫn: 

    Phương pháp vẽ đồ thị hàm số bậc nhất  y=ax+b.

 - Cho x=0 thì y=b ta được điểm A( 0;b) thuộc trục tung Oy.

 - Cho y=0 thì \(x=- \frac{b}{a} \) ta được điểm \(B(- \frac{b}{a}; 0)\) thuộc trục hoành Ox.

   Vẽ đường thẳng qua A,B ta được đồ thị của hàm số y=ax+b.

* Trường hợp đặc biệt: Nếu \(B\equiv A\) thì cho x=1 \(\Rightarrow\) B(1; a+b)

     Giải: 

   a) Đồ thị hàm số: y=2x là đường thẳng đi qua hai điểm O(0;0) và M(1;2)

   Đồ thị hàm số y =2x+5 là đường thẳng đi qua hai điểm P(0;5) và \( Q( -\frac{5}{2};0)\)

   b) Đồ thị hàm số \(y= -\frac{2}{3}x\) là đường thẳng đi qua hai điểm 0(0;0) và N(1; \(- \frac{2}{3}\))

   Đồ thị hàm số \(y= -\frac{2}{3}x\) là đường thẳng đi qua hai điểm O(0;5) và N\(N(\frac{15}{2};0)\)

  c) Bốn đường thẳng đã cho cắt nhau tạo thành tứ giác OABC.

   Vì đường thẳng y=2x+5 song song với đường thẳng y =2x và đường \(y=-\frac{2}{3}x\) song song với đường thẳng \(y= - \frac{2}{3}x+5\)

  Nên tứ giác OABC là hình bình hành do có hai cặp cạnh đối song song.