Đề kiểm tra 15 phút - Đề số 4 - Bài 5 - Chương 2 - Đại số 9

Đề bài

Bài 1. Tính góc tạo bởi đường thẳng (d) : \(y = 2x + 1\) và trục \(Ox\) (làm tròn đến phút)

Bài 2. Cho đường thẳng (d): \(y = x\). Viết phương trình đường thẳng (d’) qua điểm \(M(1; 1)\) và vuông góc với đường thẳng (d).

Hướng dẫn giải

Bài 1. Vẽ đường thẳng \(y = 2x + 1\).

Đường thẳng y = \(2x + 1\) qua hai điểm \(A(0; 1)\) và \(B\left( { - {1 \over 2};0} \right)\)

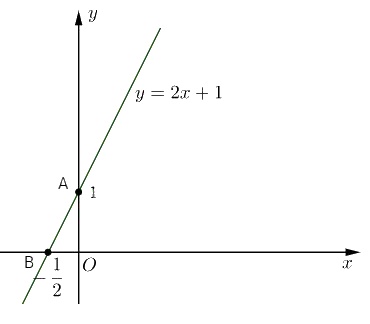
Trong tam giác vuông OAB, ta có:

\(OA = 2;OB = \left| { - {1 \over 2}} \right| = {1 \over 2}\)

Vậy : \(\tan \alpha  = {{OA} \over {OB}} = 2 \Rightarrow \alpha  \approx 63^\circ 26'\)

Bài 2. Vẽ đường thẳng d: \( y = x\)

Ta tìm được góc giữa đường thẳng (d) và \(Ox\) là \(α\) và \(\tanα = 1 ⇒ α = 45^o\)

Đường thẳng (d’) qua M và vuông góc với (d) cắt Ox tại N

Ta có: \(\widehat {OMN} = 90^\circ \) và \(\widehat {MON} = 45^\circ  \)

\(\Rightarrow \widehat {ONM} = 45^\circ  \Rightarrow \widehat {MNx} = 135^\circ \)

Vậy hệ số góc của (d’) bằng \(a = \tan135^o = -1\)

Phương trình của (d’) có dạng : \(y = -x + b\)

\(M \in \left( {d'} \right) \Rightarrow 1 =  - 1 + b \Rightarrow b = 2\)

Vậy: \(y = -x + 2\) là phương trình của (d’)