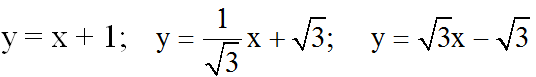Giải bài 31 trang 59 - Sách giáo khoa Toán 9 tập 1

Đề bài

       a) Vẽ đồ thị của các hàm số

     b) Gọi α, β, γ lần lượt là các góc tạo bởi các đường thẳng trên trục Ox.

   Chứng minh rằng

 

   Tính số đo các góc α, β, γ.

Hướng dẫn giải

       Hướng dẫn:

   Vẽ đồ thị của các hàm số trên cùng một hệ trục tọa độ, rồi dùng hệ thức lượng giác trong tam giác vuông để tính \(tg \alpha , tg\beta, tg \gamma\) từ đó suy ra số đo góc \(\alpha; \beta; \gamma\)

        Giải: 

      a) Đường thẳng y= x+1 đi qua điểm A(0;1) và B(-1;0).

   Đường thẳng \( y = \frac{1}{\sqrt{3}}+ \sqrt{3}\) đi qua hai điểm \(C(0; \sqrt{3})\) và D( -3;0)

   Đường thẳng \(y =\sqrt{3} x-\sqrt{3}\) đi qua hai điểm \(E(0;- \sqrt{3})\) và F(1;0)

   

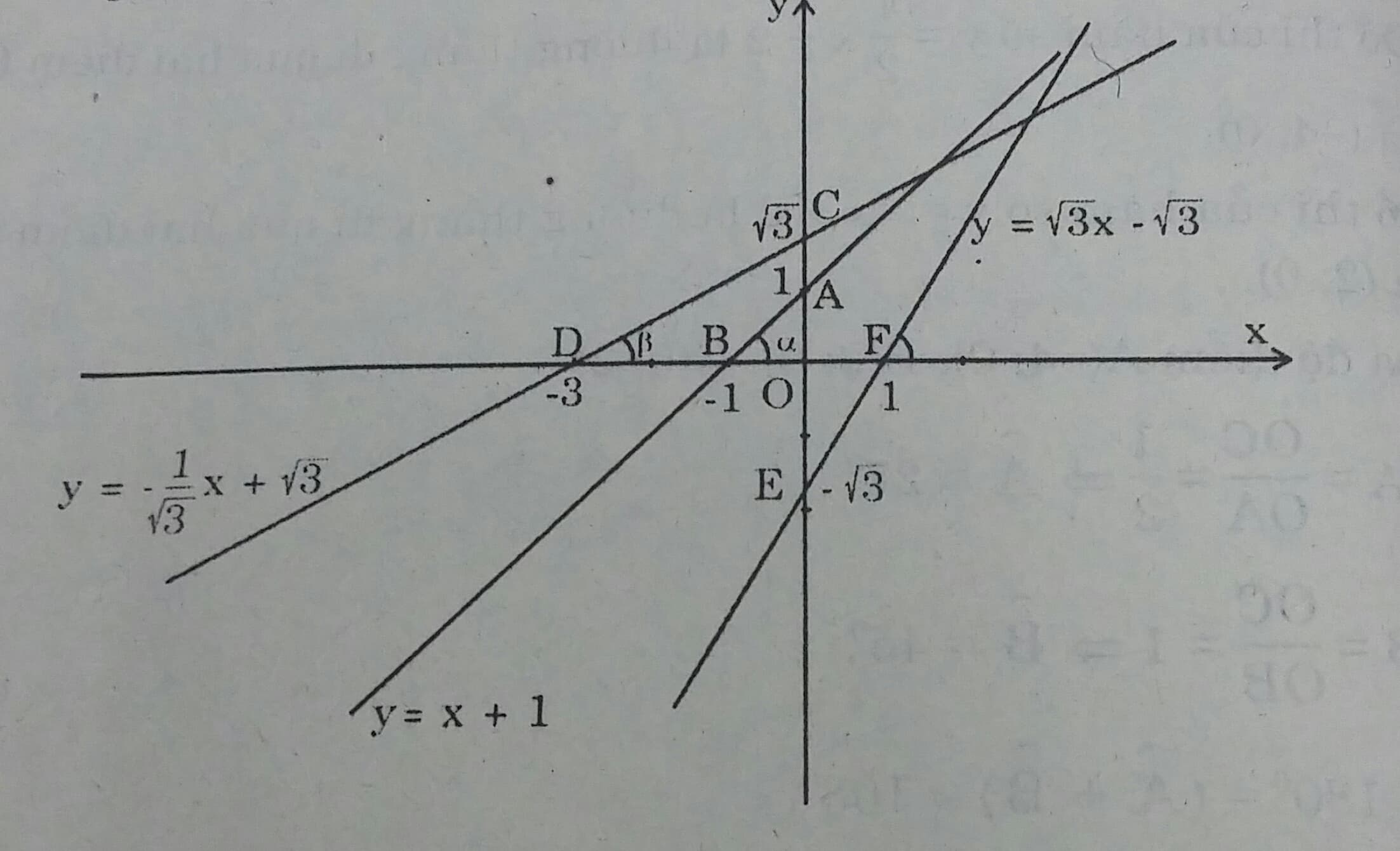
     b) Xét tam giác vuông OAB, ta có: \(tg \alpha \frac{OA}{OB}=1\)

   Xét tam giác vuông OCD, ta có: \( tg \beta = \frac{OC}{OD}= \frac{\sqrt{3}}{3}= \frac{1}{\sqrt{3}}\)

   Xét tam giác vuông OEF, ta có: \(\widehat{OFE}= \gamma\)( đối đỉnh) 

   \(tg \gamma = tag \widehat{OFE}= \frac{OE}{OF}= \sqrt{3}\)

   Từ đó tính được: \( \alpha =45^0; \beta= 30^0; \gamma= 60^0\)