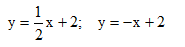Giải bài 30 trang 59 - Sách giáo khoa Toán 9 tập 1
Tóm tắt bài
Đề bài
a) Vẽ trên cùng một mặt phẳng tọa độ đồ thị của các hàm số sau:
b) Gọi giao điểm của hai đường thẳng
với trục hoành theo thứ tự là A, B và gọi giao điểm của hai đường thẳng đó là C.
Tính các góc của tam giác ABC (làm tròn đến độ)
c) Tính chu vi và diện tích của tam giác ABC (đơn vị đo trên các trục tọa độ là xentimet).
Hướng dẫn giải
Hướng dẫn
- Vẽ đồ thị của các hàm số \(y =\frac{1}{2}x+ 2\) và \(y =-x+2\) từ đó xác định các điểm A,B,C trên hình vẽ.
- Sử dụng các hệ thức lượng trong tác giác vuông và định lý Py-ta-go để tính các góc, các cạnh và đường cao trong tam giác.
* Lưu ý:
Diện tích tam giác \(S= \frac{1}{2}x\) độ dài đáy x độ dài đường cao.
Giải:
.jpg)
Đồ thị hàm số \( y = \frac{1}{2}x+ 2\) là đường thẳng đi qua hai điểm (0;2) và (-4;0).
Đồ thị của hàm số y=-x+2 là đường thẳng đi qua hai điểm (0;2) và (2;0)
b) Tọa độ điểm A(-4;0), B(2;0), C(0;2)
\( tg A= \frac{OC}{OA}=\frac{1}{2} \Rightarrow \widehat{A} \approx 27^0\)
\( tg B= \frac{OC}{OB}=1\Rightarrow \widehat{A} = 45^0\)
\(\widehat{C}= 180^0-(\widehat{A}+\widehat{B}) \approx 108^0\)
c) Áp dụng định lý py-ta-go đối với các tam giác vuông OAC và OBC:
\(AC=\sqrt{OA ^2+OC^2}=\sqrt{4^2+ 2^2}=\sqrt{20}(cm)\)
\(BC=\sqrt{OB ^2+OC^2}=\sqrt{2^2+ 2^2}=\sqrt{8}(cm)\)
AB= OA+ OB=4+2=6(cm)
Chu vi tam giác ABC là: P= AB+BC+CA= \(6+ \sqrt{20}+\sqrt{8} \approx 13,3(cm)\)
Diện tích tam giác ABC là: \(S= \frac{1}{2}AB.OC=\frac{1}{2}.6.2(cm^2) \)
Copyright © 2021 HOCTAP247