Bài 10 trang 104 SGK Toán 9 tập 1
Tóm tắt bài
Đề bài
Cho tam giác \(ABC\), các đường cao \(BD\) và \(CE\). Chứng minh rằng:
a) Bốn điểm \(B,\ E,\ D,\ C\) cùng thuộc một đường tròn.
b) \(DE < BC\)
Hướng dẫn giải
a) Sử dụng tính chất: Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền thì bằng nửa cạnh đó để chứng minh ba đỉnh của tam giác vuông nằm trên đường tròn đường kính là cạnh huyền.
b) Sử dụng định lí: Trong các dây của đường tròn, dây lớn nhất là đường kính.
Lời giải chi tiết
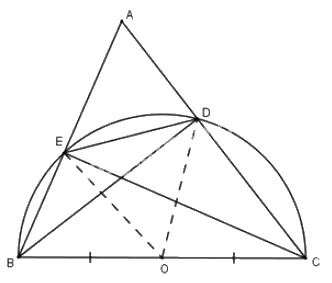
a) Gọi \(O\) là trung điểm của \(BC \Rightarrow OB=OC=\dfrac{BC}{2}.\) (1)
Vì \(DO\) là đường trung tuyến của tam giác vuông \(DBC\).
Theo tính chất trung tuyến ứng với cạnh huyền, ta có:
\(OD=\dfrac{1}{2}BC \) (2)
Từ (1) và (2) suy ra \(OD=OB=OC=\dfrac{1}{2}BC\)
Do đó ba điểm \(B,\ D,\ C\) cùng thuộc đường tròn tâm \(O\) bán kính \(OB\).
Lập luận tương tự, ta có ba điểm \(B,\ E,\ C\) cùng thuộc đường tròn tâm \(O\) bán kính \(OB\).
Do đó 4 điểm \(B,\ C,\ D,\ E\) cùng thuộc đường tròn \((O)\) đường kính \(BC\).
b) Xét đường \({\left( O; \dfrac{BC}{2} \right)}\), với \(BC\) là đường kính.
Ta có \(DE\) là một dây cung không đi qua tâm, theo định lí 1, ta có \(BC > DE\).
Copyright © 2021 HOCTAP247
