Bài 11 trang 104 SGK Toán 9 tập 1
Tóm tắt bài
Đề bài
Cho đường tròn \((O)\) đường kính \(AB\), dây \(CD\) không cắt đường kính \(AB\). Gọi \(H\) và \(K\) theo thứ tự là chân các đường vuông góc kẻ từ \(A\) và \(B\) đến \(CD\). Chứng minh rằng \(CH=DK\)
Gợi ý: Kẻ \(OM\) vuông góc với \(CD\).
Hướng dẫn giải
+) Kẻ đườnh kính vuông góc với dây.
+) Sử dụng tính chất: trong một đường tròn, đường kính vuông góc với dây thì đi qua trung điểm của dây.
+) Trong hình thang, đường thẳng song song với hai đáy và đi qua trung điểm của một cạnh bên thì đi qua trung điểm của cạnh bên còn lại.
Lời giải chi tiết
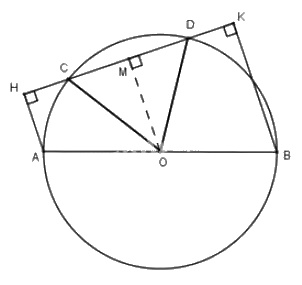
Vẽ \(OM \bot CD\)
Theo tính ĐL 2- trang 103, ta có: \( MC=MD\) (1)
Tứ giác \(AHKB\) có \(AH \bot HK;\ BK \bot HK \Rightarrow HA // BK\).
Suy ra tứ giác \(AHKB\) là hình thang.
Xét hình thang \(AHKB\), ta có:
\(OM // AH //BK\) (cùng vuông góc với \(CD\))
mà \(AO=BO=\dfrac{AB}{2}\)
\(\Rightarrow MO\) là đường trung bình của hình thang \(AHKB\).
\(\Rightarrow MH=MK\) (2)
Từ (1) và (2) \(\Rightarrow MH-MC=MK-MD \Leftrightarrow CH=DK.\)
Nhận xét: Kết quả của bài toán trên không thay đổi nếu ta đổi chỗ hai điểm \(C\) và \(D\) cho nhau
Copyright © 2021 HOCTAP247
