Trang chủ
Lớp 9
Toán Lớp 9 SGK Cũ
Bài 2. Đường kính và dây của đường tròn
Giải bài 10 trang 104 - Sách giáo khoa Toán 9 tập 1
Giải bài 10 trang 104 - Sách giáo khoa Toán 9 tập 1
Lý thuyết
Bài tập
Mục lục
Tóm tắt bài
Đề bài
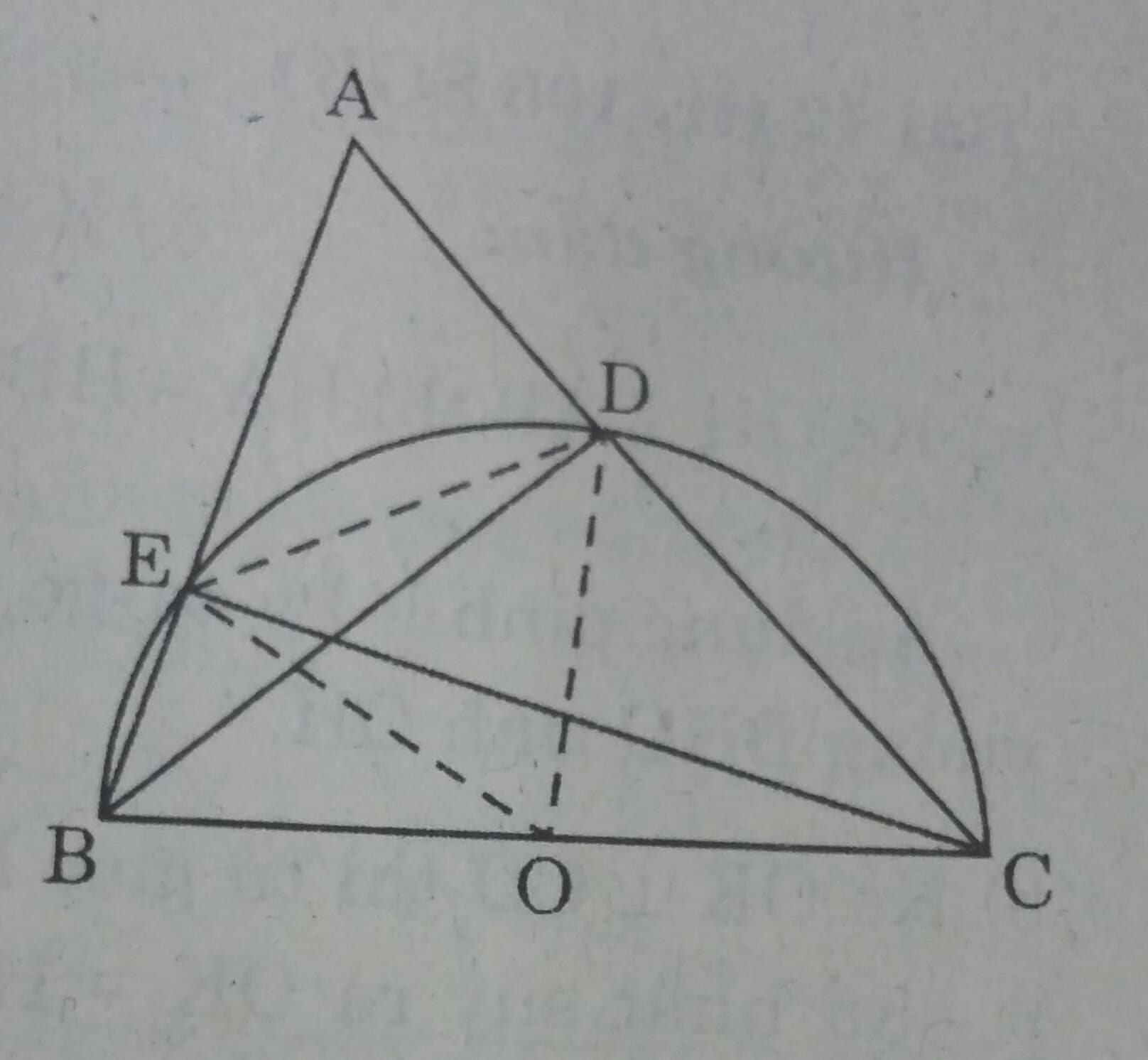
Cho tam giác ABC, các đường cao BD và CE. Chứng minh rằng:
a) Bốn điểm B, E, D, C cùng thuộc một đường tròn.
b) DE < BC.
Hướng dẫn giải
Hướng dẫn:
a) Muốn chứng minh bốn điểm cùng thuộc một đường tròn ta chứng minh bố điểm đó cách đều một điểm.
b) Trong các dây của đường tròn, đường kính là dây lớn nhất.
Giải:
a) Gọi O là trung điểm của BC.
\(\Delta BDC\) vuông tại D nên \(OD= \frac{1}{2}BC\)
\(\Delta BEC\) vuông tại D nên \(OE= \frac{1}{2}BC\)
Suy ra: OB= OC= OD= OE
Do đó 4 điểm B,C,D,E cùng thuộc một đường tròn có đường kính là BC.
b) Trong đường tròn nói trên, DE là một dây không đi qua tâm, DE là một dây không đi qua tâm, BC là đường kính nên BC> DE.
Copyright © 2021 HOCTAP247
