Bài 19 trang 110 SGK Toán 9 tập 1
Tóm tắt bài
Đề bài
Cho đường thẳng \(xy\). Tâm của các đường tròn có bán kính \(1cm\) và tiếp xúc với đường thẳng \(xy\) nằm trên đường nào?
Hướng dẫn giải
+) Xác định xem tâm đường tròn cách đường thẳng cho trước một khoảng là bao nhiêu.
+) Vận dụng tính chất: Tập hợp các điểm cách đường thẳng \(d\) một khoảng \(a(cm)\) là đường thẳng song song với \(d\) và cách \(d\) là \(a(cm)\).
Lời giải chi tiết
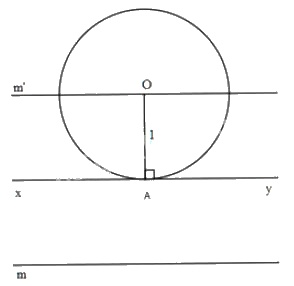
Gọi \(O\) là tâm của đường tròn bán kính \(1cm\) và tiếp xúc với đường thẳng \(xy\).
Vì \(R=1cm\) nên điểm \(O\) cách đường thẳng \(xy\) là \(1cm\).
Ta có: tập hợp các điểm cách \(xy\) một khoảng bằng \(1cm\) là đường thẳng song song với \(xy\) và cách \(xy\) là \(1cm\). Ta có thể vẽ được \(2\) đường thẳng thỏa mãn yêu cầu đó.
Do vậy, \(O\) có thể nằm trên hai đường thẳng \(m\) và \(m'\) song song với \(xy\) và cách \(xy\) là \(1cm\).
Copyright © 2021 HOCTAP247
