Đề kiểm tra 15 phút - Đề số 2 - Bài 4 - Chương 2 - Hình học 9

Đề bài

Cho ∆ABC vuông tại A có \(AB = 3cm, AC = 4cm\). Vẽ đường tròn tâm A bán kính 2,8cm. Hãy xác định vị trí tương đối của đường thẳng BC và đường tròn (A; 2,8cm)

Hướng dẫn giải

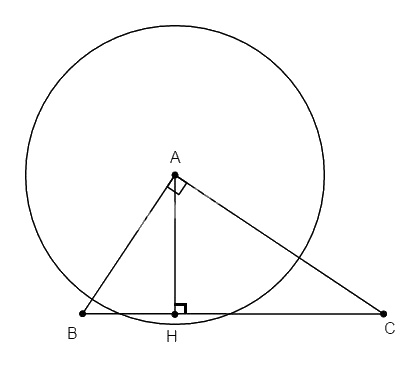
Kẻ \(AH ⊥ BC\). Trong tam giác vuông ABC, ta có:
\({1 \over {A{H^2}}} = {1 \over {A{B^2}}} + {1 \over {A{C^2}}}\) (định lí 4)

hay \({1 \over {A{H^2}}} = {1 \over {{3^2}}} + {1 \over {{4^2}}} = {{25} \over {144}}\)

\(\Rightarrow {1 \over {AH}} = {5 \over {12}} \Rightarrow AH = 2,4cm\)

Ta có: \(2,4

Do đó đường thẳng BC và (A; 2,8cm) cắt nhau.