Đề kiểm 15 phút - Đề số 1 - Bài 1 - Chương 3 - Đại số 9
Tóm tắt bài
Đề bài
Bài 1: Viết công thức nghiệm tổng quát và vẽ đường thẳng diễn tập nghiệm của phương trình :
\(3x – y = 6.\)
Bài 2: Cho hai phương trình :\(2x – 3y = 1\) và \(x – y = 1\). Vẽ hai đường thẳng biểu diễn tập nghiệm của mỗi phương trình trên cùng một hệ trục tọa độ. Xác định tọa độ giao điểm của hai đường thẳng đó.
Hướng dẫn giải
Bài 1. Ta có : \(y = 3x – 6.\)
Vậy công thức nghiệm tổng quát là: \((x;3x-6)\)
Bảng giá trị :
x
0
2
y
−6
0
x
0
2
y
−6
0
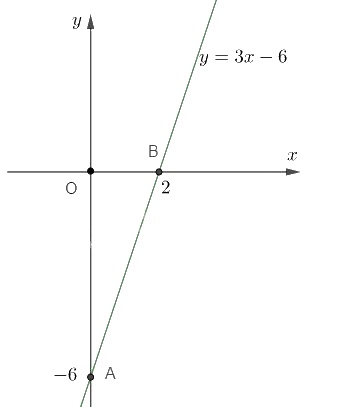
Đường thẳng \(y = 3x – 6\) qua hai điểm : \(A(0; −6)\) và \(B(2; 0 ).\)
Bài 2:
Vẽ đường thẳng \(2x – 3y = 1\) \( \Leftrightarrow y = {2 \over 3}x - {1 \over 3}\)
Bảng giá trị :
x
0
2
y
\( - {1 \over 3}\)
1
x
0
2
y
\( - {1 \over 3}\)
1
Đường thẳng (d) qua hai điểm : \(\left( {0; - {1 \over 3}} \right)\) và ( 2; 1).
Vẽ đường thẳng \(x - y = 1 \Rightarrow y = x – 1\)
Bảng giá trị :
x
0
1
y
−1
0
x
0
1
y
−1
0
Đường thẳng (d’) qua hai điểm : \(( 0; -1)\) và \(( 1; 0)\).
\({2 \over 3}x - {1 \over 3} = x - 1 \)
\(\Leftrightarrow 2x - 1 = 3x - 3 \Leftrightarrow x = 2\)
Thế \(x = 2\) vào phương trình : \(y = x – 1\)
Tọa độ giao điểm : \(( 2; 1).\)
Copyright © 2021 HOCTAP247
