Giải bài 3 trang 7 - Sách giáo khoa Toán 9 tập 2
Tóm tắt bài
Đề bài
Cho hai phương trình x + 2y = 4 và x – y = 1. Vẽ hai đường thẳng biểu diễn tập nghiệm của hai phương trình đó trên cùng một hệ tọa độ. Xác định tọa độ giao điểm của hai đường thẳng và cho biết tọa độ của nó là nghiệm của các phương trình nào.
- Vẽ đường thẳng x + 2y = 4.
+ Cho x = 0 => y = 2 được A(0; 2).
+ Cho y = 0 => x = 4 được B(4; 0).
Đường thẳng cần vẽ là đường thẳng (d1) qua A, B.
Hướng dẫn giải
Giải:
Nghiệm tổng quát của phương trình x + 2y = 4 là: \(\left\{\begin{matrix}y=-\dfrac{1}{2}x+2\\ x \in R\end{matrix}\right.\)
Đường thẳng biểu diễn tập nghiệm của phương trình \(y=-\dfrac{1}{2}x+2\).
Cho x = 0 thì y = 2, ta xác định được điểm A(0; 2).
Cho y = 0 thì x = 4, ta xác định được điểm B(4; 0).
Vẽ đường thẳng AB.
Nghiệm tổng quát của phương trình x - y = 1 là: \(\left\{\begin{matrix}y=x-1\\ x \in R\end{matrix}\right.\)
Đường thẳng biểu diễn tập nghiệm của phương trình y = x - 1.
Cho x = 0 thì y = -1, ta xác định được điểm C(0; 2).
Cho y = 0 thì x = 1, ta xác định được điểm D(1; 0).
Vẽ đường thẳng CD.
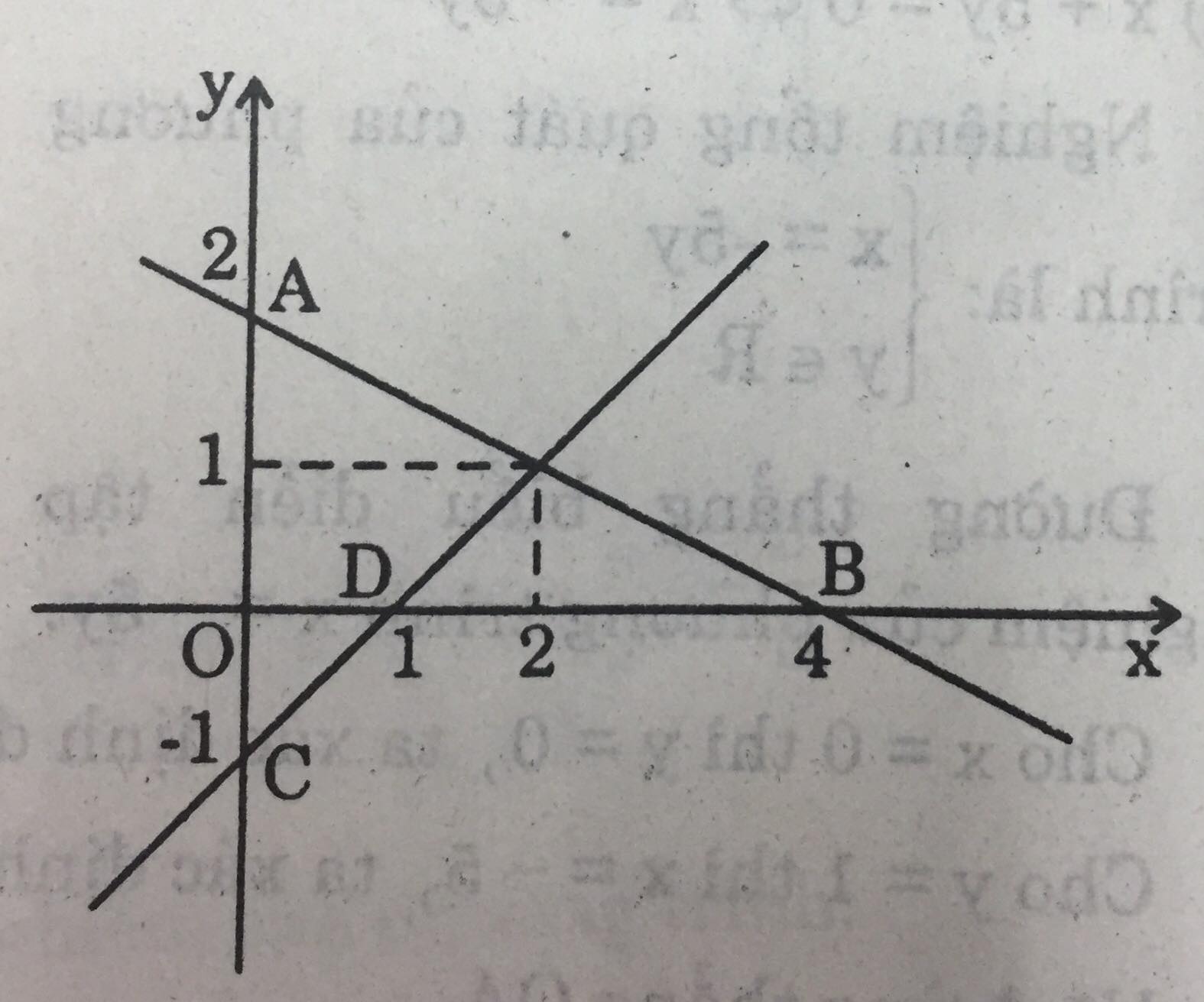
Giao điểm của hai đường thẳng có tọa độ (2; 1). Đó là nghiệm của cả hai phương trình đã cho.
Copyright © 2021 HOCTAP247
