Bài 2 trang 49 SGK Đại số 10
Tóm tắt bài
Đề bài
Lập bảng biến thiên và vẽ đồ thị của các hàm số.
a) \(y = 3x^2- 4x + 1\);
b) \(y = - 3x^2+ 2x – 1\);
c) \(y = 4x^2- 4x + 1\);
d) \(y = - x^2+ 4x – 4\);
e) \(y = 2x^2+ x + 1\);
f) \(y = - x^2+ x - 1\).
Hướng dẫn giải
Dựa vào đồ thị của hàm số \(y= a x^2 + bx + c\) ( a khác 0), ta có bảng biến thiên của nó trong hai trường hợp a > 0 và a
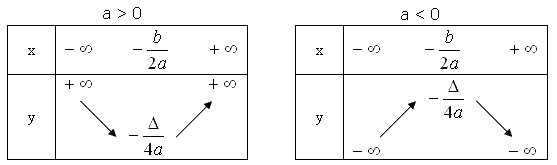
Cách vẽ:
Bước 1: Xác định tọa độ của đỉnh \(I\left( { - \frac{b}{{2a}}; - \frac{\Delta }{{4a}}} \right)\)
Bước 2: Vẽ trục đối xứng \(x = - \frac{b}{{2a}}\)
Bước 3: Xác định tọa độ các giao điểm của parabol với trục tung, trục hoành ( nếu có)
Xác định thêm một số điểm thuộc đồ thị để vẽ đồ thị chính xác hơn.
4) Vẽ parabol
Khi vẽ parabol cần lưu ý đến dấu của hệ số a (a > 0 thì bề lõm quay lên trên); (a > 0 thì bề lõm quay xuống dưới).
Lời giải chi tiết
a) \(y = 3x^2- 4x + 1\)
Bảng biến thiên:
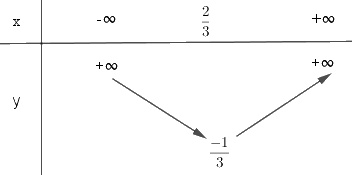
Đồ thị:
- Đỉnh: \(I\left( {{2 \over 3}; - {1 \over 3}} \right)\)
- Trục đối xứng: \(x = {2 \over 3}\)
- Giao điểm với trục tung \(A(0; 1)\)
- Giao điểm với trục hoành \(B\left( {{1 \over 3};0} \right)\), \(C(1; 0)\).
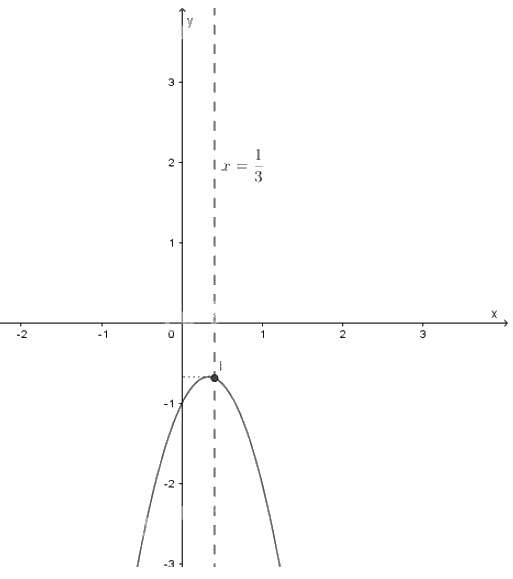
b) \(y = - 3x^2+ 2x – 1\)
Bảng biến thiên:
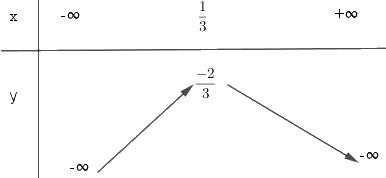
Vẽ đồ thị:
- Đỉnh \(I\left( {{1 \over 3}; - {2 \over 3}} \right)\), trục đối xứng: \(x = {1 \over 3}\)
- Giao điểm với trục tung \(A(0;- 1)\).
- Giao điểm với trục hoành: không có.
Ta xác định thêm điểm phụ: \(B(1;- 2)\), \(C(1;- 6)\).
c) \(y = 4x^2- 4x + 1\).
Lập bảng biến thiên và vẽ tương tự câu a, b.
d) \(y = - x^2+ 4x – 4=- (x – 2)^2\)
Bảng biến thiên:
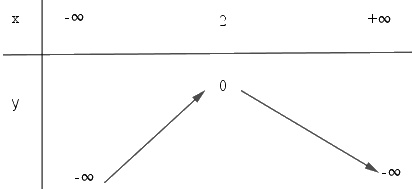
Cách vẽ đồ thị:
Ngoài cách vẽ như câu a, b, ta có thể vẽ như sau:
+ Vẽ đồ thị \((P)\) của hàm số \(y = - x^2\).
+ Tịnh tiến \((P)\) song song với \(Ox\) sang phải \(2\) đơn vị được \((P1)\) là đồ thị cần vẽ. (hình dưới).
e) \(y = 2x^2+ x + 1\);
- Đỉnh \(I\left( {{{ - 1} \over 4};{{ - 7} \over 8}} \right)\)
- Trục đối xứng : \(x = {{ - 1} \over 4}\)
- Giao \(Ox\): Đồ thị không giao với trục hoành
- Giao \(Oy\): Giao với trục tung tại điểm \((0;1)\)
Bảng biến thiên:
Vẽ đồ thị theo bảng sau:
x
-2
-1
0
1
2
y
7
2
1
4
11
x
-2
-1
0
1
2
y
7
2
1
4
11
f) \(y = - x^2+ x - 1\).
- Đỉnh \(I\left( {{1 \over 2};{{ - 3} \over 4}} \right)\)
- Trục đối xứng : \(x = {1 \over 2}\)
- Giao Ox: Đồ thị không giao với trục hoành
- Giao Oy: Giao với trục tung tại điểm \((0;-1)\)
Bảng biến thiên:
Vẽ đồ thị theo bảng sau:
x
-2
-1
0
1
2
y
-7
-3
-1
-1
-3
x
-2
-1
0
1
2
y
-7
-3
-1
-1
-3
Copyright © 2021 HOCTAP247
