- Nếu mọi phần tử của tập hợp A đều thuộc tập hợp B thì tập hợp A gọi là tập hợp con của tập hợp B. Kí hiệu: A \(\subset\) B đọc là: A là tập hợp con của tập hợp B hoặc A được chứa trong B hoặc B chứa A.

- Mỗi tập hợp đều là tập hợp con của chính nó và tập hợp rỗng là tập hợp con của mọi tập hợp.

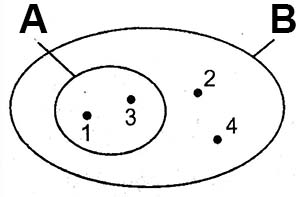
H2: Minh họa tập hợp A là tập hợp con của tập hợp B

* Cách tìm số tập hợp con của một tập hợp: Nếu A có n phần tử thì số tập hợp con của tập hợp A là 2ⁿ.

Bài 1: Cho tập hợp A là các chữ cái trong cụm từ “Thành phố Hồ Chí Minh”

a. Hãy liệt kê các phần tử của tập hợp A.

b. Điền kí hiệu thích hợp vào ô vuông

b [ ] A; c [ ] A; h [ ] A

Hướng dẫn

a/ A = {a, c, h, i, m, n, ô, p, t}

b/ b \(\notin\) A ; c \(\in\) A; h\(\in\) A

Lưu ý HS: Bài toán trên không phân biệt chữ in hoa và chữ in thường trong cụm từ đã cho.

Bài 2: Cho tập hợp các chữ cái X = {A, C, O}

a/ Tìm cụm chữ tạo thành từ các chữ của tập hợp X.

b/ Viết tập hợp X bằng cách chỉ ra các tính chất đặc trưng cho các phần tử của X.

Hướng dẫn

a/ Chẳng hạn cụm từ “CA CAO”

b/ X = {x: x-chữ cái trong cụm chữ “CA CAO”}

Bài 3: Cho tập hợp A = {1; 2;3;x; a; b}

a/ Hãy chỉ rõ các tập hợp con của A có 1 phần tử.

b/ Hãy chỉ rõ các tập hợp con của A có 2 phần tử.

c/ Tập hợp B = {a, b, c} có phải là tập hợp con của A không?

Hướng dẫn

a/ {1} { 2} { a } { b} ….

b/ {1; 2} {1; a} {1; b} {2; a} {2; b} { a; b} ……

c/ Tập hợp B không phải là tập hợp con của tập hợp A bởi vì tập hợp B có phần tử c nhưng phần tử c lại không thuộc tập hợp A

Bài 4: Cho tập hợp B = {a, b, c}. Hỏi tập hợp B có tất cả bao nhiêu tập hợp con?

Hướng dẫn

- Tập hợp con của B không có phần từ nào là 1: \(\emptyset\)

- Các tập hợp con của B có một phần tử là 3: {a}, {b}, {c}

- Các tập hợp con của B có hai phần tử là 3: {a,b}, {a,c}, {b,c}

- Tập hợp con của B có 3 phần tử chính là 1: {a, b, c}

Vậy tập hợp A có tất cả là 1+3+3+1 = 8 tập hợp con = 2³

Ghi chú: Một tập hợp A bất kỳ luôn có hai tập hợp con đặc biệt là tập hợp rỗng và chính tập hợp A. Nếu A có n phần tử thì số tập hợp con của tập hợp A là 2ⁿ.

3. Luyện tập Bài 1 Chương 1 Số học 6 Tập 1

Qua bài giảng Tập hợp và phần tử của tập hợp này, các em cần hoàn thành 1 số mục tiêu mà bài đưa ra như :

Phát biểu được định nghĩa tập hợp, phần tử của tập hợp.
Cách viết các kí hiệu
Cách liệt kê các phần tử trong tập hợp

3.1 Trắc nghiệm về tập hợp và phần tử của tập hợp

Để cũng cố bài học xin mời các em cũng làm Bài kiểm tra Trắc nghiệm Toán 6 Chương 1 Bài 1 để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.

Câu 1:
Số liền trước số 11 là:
- A. 10
- B. 9
- C. 11
- D. 12
Câu 2:
Tập hợp các số tự nhiên không vượt quá 5 gồm bao nhiêu phần tử?
- A. 4 phần tử
- B. 5 phần tử
- C. 6 phần tử
- D. 7 phần tử
Câu 3:
Tập hợp các phần tử trong câu " HOCTAP247" gồm bao nhiêu phần tử
- A. 4 phần tử
- B. 5 phần tử
- C. 6 phần tử
- D. 7 phần tử

Câu 2- Câu 5: Xem thêm phần trắc nghiệm để làm thử Online

3.2 Bài tập SGK về Tập hợp và số phần tử của tập hợp

Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Toán 6 Chương 1 Bài 1 sẽ giúp các em nắm được các phương pháp giải bài tập từ SGK Toán 6 tập 1

Bài tập 5 trang 6 SGK Toán 6 Tập 1

Bài tập 1 trang 5 SBT Toán 6 Tập 1

Bài tập 2 trang 5 SBT Toán 6 Tập 1

Bài tập 3 trang 5 SBT Toán 6 Tập 1

Bài tập 4 trang 5 SBT Toán 6 Tập 1

Bài tập 5 trang 5 SBT Toán 6 Tập 1

Bài tập 6 trang 5 SBT Toán 6 Tập 1

Bài tập 7 trang 5 SBT Toán 6 Tập 1

Bài tập 8 trang 6 SBT Toán 6 Tập 1

Bài tập 9 trang 5 SBT Toán 6 Tập 1

Bài tập 1.1 trang 6 SBT Toán 6 Tập 1

Bài tập 1.2 trang 7 SBT Toán 6 Tập 1