Bài 1 trang 34 SGK Hình học 11

Đề bài

Cho lục giác đều \(ABCDEF\) tâm \(O\). Tìm ảnh của tam giác \(AOF\).

a) Qua phép tịnh tiến theo vectơ \(AB\)

b) Qua phép đối xứng qua đường thẳng \(BE\)

c) Qua phép quay tâm \(O\) góc \( 120^{\circ}\)

Hướng dẫn giải

Dựa vài khái niệm các phép dời hình.

Lời giải chi tiết

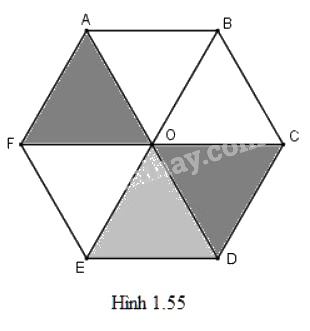
a) Ta có: 

\(\left\{ \begin{array}{l}
{T_{\overrightarrow {AB} }}\left( A \right) = B\\
{T_{\overrightarrow {AB} }}\left( O \right) = C\\
{T_{\overrightarrow {AB} }}\left( F \right) = O
\end{array} \right. \Rightarrow {T_{\overrightarrow {AB} }}\left( {\Delta AOF} \right) = \Delta BCO\)

b) Ta có:

\(\left\{ \begin{array}{l}
{D_{BE}}\left( A \right) = C\\
{D_{BE}}\left( O \right) = O\\
{D_{BE}}\left( F \right) = D
\end{array} \right. \Rightarrow {D_{BE}}\left( {\Delta AOF} \right) = COD\)

c) Ta có:

\(\left\{ \begin{array}{l}
{Q_{\left( {O;{{120}^0}} \right)}}\left( A \right) = E\\
{Q_{\left( {O;{{120}^0}} \right)}}\left( O \right) = O\\
{Q_{\left( {O;{{120}^0}} \right)}}\left( F \right) = D
\end{array} \right. \\\Rightarrow {Q_{\left( {O;{{120}^0}} \right)}}\left( {\Delta AOF} \right) = \Delta EOD\)