Bài 1 trang 97 SGK Hình học 11
Tóm tắt bài
Đề bài
Cho hình lập phương \(ABCD.EFGH\). Hãy xác định góc giữa các cặp vectơ sau đây:
a) \(\overrightarrow{AB}\) và \(\overrightarrow{EG};\)
b) \(\overrightarrow{AF}\) và \(\overrightarrow{EG};\)
c) \(\overrightarrow{EG}\) và \(\overrightarrow{DH}.\)
Hướng dẫn giải
Sử dụng định nghĩa góc giữa hai vector trong không gian.
Lời giải chi tiết
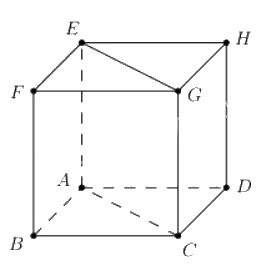
a) \((\widehat{\overrightarrow{AB}, \overrightarrow{EG}})\) \(=(\widehat{\overrightarrow{AB}, \overrightarrow{AC}})\)\(=45^{0};\)
b) \(\widehat{(\overrightarrow{AF}, \overrightarrow{EG})}\)\(=\widehat{(\overrightarrow{DG}, \overrightarrow{EG})}\) \(= 60^{0};\) (Vì tam giác \(DGE\) là tam giác đều)
c) \((\widehat{\overrightarrow{AB}, \overrightarrow{DH}})\) \(= 90^{0}.\) (Vì \(DH\bot (ABCD))\)
Copyright © 2021 HOCTAP247
